Unbeschränktes und logistisches Wachstum (Differenzialgleichungen)

Eine Population bestehe aus N Individuen. Nach einer Zeit $Δ t$ ist eine Änderung $Δ N$ mit $Δ N = N (t + Δ t) - N (t)$ des Populationsumfangs N zu verzeichnen. Kann die Population ohne Beschränkung wachsen, so ist die Änderung proportional zum Ausgangsumfang – je mehr Individuen vorhanden sind, desto mehr Nachwuchs stellt sich ein. Es gilt also $Δ N \sim N oder Δ N = k N$ (unbeschränktes Wachstum), wobei k als Wachstumsrate (bei unbeschränktem Wachstum) bezeichnet wird.
Ist das Wachstum durch eine Obergrenze G der Individuenzahl beschränkt, so wird sich bei noch kleiner Individuenzahl ein annähernd unbeschränktes Wachstum einstellen, mit wachsender Zahl N wird die Wachstumsrate jedoch kleiner, um schließlich bei $N = G$ den Wert 0 anzunehmen. Eine Beschränkung kommt beispielsweise zustande, wenn die Population in einem isolierten Gebiet lebt, in dem sich höchstens G Individuen ernähren können.

Die modifizierte Wachstumsrate
$k_{b} = k (1 - \frac{N}{G})$
weist das erwartete Verhalten auf.

Als Differenzengleichung ergibt sich
$Δ N = k_{b} \cdot N = k \cdot (1 - \frac{N}{G}) \cdot N$
(logistisches Wachstum).

Die Gleichung des logistischen Wachstums wurde erstmals von VERHULST und PEARL im Jahre 1838 verwendet.

Da sich in beiden Wachstumsfällen die Änderung $Δ N$ auf einen bestimmten Zeitraum, z.B. $Δ t = 1 Jahr$ , bezieht, spielt die Art des Populationswachstums innerhalb dieses Zeitraums keine Rolle. Es könnte sich - wie bei Bakterien - um ein kontinuierliches Wachstum handeln.
Möglich wäre aber auch, dass ein an einen Lebenszyklus gebundenes diskontinuierliches Populationswachstum - wie bei Schmetterlingen - vorliegt. Im Falle des kontinuierlichen Wachstums kann man von der Differenzengleichung zu einer Differenzialgleichung übergehen.

Lösen der Differenzialgleichung des unbeschränkten Wachstums

Die Gleichung $N' (t) = r N (t), r \in ℝ, r > 0$ ist eine lineare homogene Differentialgleichung 1. Ordnung. Ihre allgemeine Lösung erhält man durch Trennen der Variablen:
$\begin{array}{l} D i e G l e i c h u n g w i r d i n d e r F o r m \frac{d N}{d t} = r N (t) g e s c h r i e b e n . \\ 1. T r e n n e n d e r V a r i a b l e n ‌ : \frac{d N}{N (t)} = r d t \\ 2. I n t e g r i e r e n ‌ : \int \frac{d N}{N (t)} = r \int d t u n d d a m i t \\ I n N = r t + c^{'}, c^{'} \in ℝ b e l . \\ 3. U m s t e l l e n n a c h N (t) ‌ : e^{\ln N} = N (t) = e^{r \cdot t + c^{'}} = e^{c^{'}} \cdot e^{r \cdot t} = c e^{r \cdot t} \\ m i t e^{c^{'}} = c, c \in ℝ, c > 0 \end{array}$
Allgemeine Lösungsfunktion ist also $N (t) = c e^{r \cdot t}$ .
Gilt die Anfangsbedingung $N (0) = N_{0}$ , so erhält man $N (0) = c e^{0} = c$ . Die Lösung des Anfangswertproblems ist daher $N (t) = N_{0} e^{r \cdot t}$ .

Lösen der Differenzialgleichung des logistischen Wachstums

Die Differentialgleichung $N' (t) = r \cdot (1 - \frac{N (t)}{G}) \cdot N (t)$ des logistischen Wachstums ist zwar auch von 1. Ordnung, aber nicht linear. Sie wird ebenfalls durch Trennen der Variablen gelöst:

1. Trennen der Variablen:

$N' (t) = \frac{d N}{d t} = r \cdot (1 - \frac{N (t)}{G}) \cdot N (t), N (0) = N_{0}$
$\frac{d N}{(1 - \frac{N (t)}{G}) \cdot N (t)} = r \cdot d t$

2. Integrieren:
$\int \frac{1}{(1 - \frac{N}{G}) \cdot N} d N = \int r d t = r t + c$

Das Integral auf der linken Seite lässt sich mittels Partialbruchzerlegung bestimmen.
Man erhält:
$\frac{1}{(1 - \frac{N}{G}) \cdot N} = \frac{1}{G - N} + \frac{1}{N}$ , also $\int \frac{1}{G - N} d N + \int \frac{1}{N} d N = - \ln (G - N) + \ln N = \ln \frac{N}{G - N} = r \cdot t + c$
(Alle Integrationskonstanten werden auf der rechten Seite zusammengefasst.)

Daraus folgt: $e^{\ln \frac{N}{G - N}} = \frac{N}{G - N} = e^{r t + c} = q \cdot e^{r t} mit q = e^{c}$
bzw. $N = (G - N) \cdot q \cdot e^{r t}$
und damit $N = \frac{G \cdot q \cdot e^{r t}}{1 + q \cdot e^{r t}}, q \in ℝ, q > 0$ .

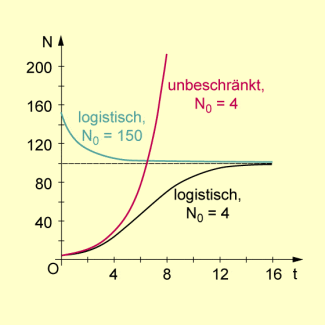
Bestimmen des Parameters q: $N_{0} = N (0) = \frac{G \cdot q}{4 + q} \Rightarrow q = \frac{N_{0}}{G - N_{0}} \Rightarrow N (t) = \frac{G N_{0} e^{r t}}{G - N_{0} + N_{0} e^{r t}}$

Für die Werte $r = 0,5 a^{- 1}$ (a ist die Zeiteinheit 1 Jahr) und $G = 100$ sind partikuläre Lösungen der Differenzialgleichungen des unbeschränkten $(N_{0} = 4)$ und des logistischen Wachstums $(N_{0} = 4 und N_{0} = 150)$ in der folgenden Abbildung dargestellt.

Grafische Darstellung partikulärer Lösungen von Differenzialgleichungen des unbeschränkten und des logistischen Wachstums

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Lernprobleme in Mathe?

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

KI-Tutor Kim hilft bei allen schulischen Problemen
Individuelle, kindgerechte Förderung in Dialogform
Lernplattform für 9 Fächer ab der 4. Klasse
Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
Rund um die Uhr für dich da

Jetzt in Mathe durchstarten

Verwandte Artikel

Angaben zum Lexikon

Impressum

Unbeschränktes und logistisches Wachstum (Differenzialgleichungen)

Lösen der Differenzialgleichung des unbeschränkten Wachstums

Lösen der Differenzialgleichung des logistischen Wachstums

Rechtliches

Einloggen