Das Runge-Kutta-Verfahren

Eine andere Möglichkeit zur Reduzierung der Abweichungen besteht darin, den Anstieg der Funktion f zwischen $x_i{\text{ und x}}_{i+1}$ besser als nur durch $G\left(x_i;{\text{ y}}_{\text{i}}\right)$ (Anstieg am Anfang des Intervalls) abzuschätzen. Hierfür lieferten die deutschen Mathematiker CARL RUNGE (1856 bis1927) und MARTIN WILHELM KUTTA (1867 bis 1944) eine weit verbreitete Variante.

Anwendung des Polygonzugverfahrens und des RUNGE-KUTTA-Verfahrens

Beispiel: Das Anfangswertproblem $f\prime \left(x\right)+f\left(x\right)=2\text{ mit }f\left(0\right)=0$ soll nach dem Polygonzugverfahren und dem RUNGE-KUTTA-Verfahren mit $h=\mathrm{0,8}$ im Intervall $\left[0;4\right]$ näherungsweise gelöst und mit der exakten Lösung $y=f\left(x\right)=-2e^{-x}+2$ verglichen werden.

Die Differenzialgleichung $f\prime \left(x\right)+f\left(x\right)=2$ wird umgewandelt in $f\prime \left(x\right)=-f\left(x\right)+2$.
Für die Funktion G gilt $G\left(x;f\left(x\right)\right)=-f\left(x\right)+2\text{ bzw}\text{. }G\left(x_i;{\overline{y}}_i\right)=-{\overline{y}}_i+2$.

• Polygonzugverfahren:
  ${\overline{y}}_{i+l}{}^{\left(poly\right)}={\overline{y}}_i{}^{\left(poly\right)}+m_i{}^{\left(poly\right)}\cdot h$
• RUNGE- KUTTA -Verfahren:
  ${\overline{y}}_{i+l}{}^{\left(ru\text{-ka}\right)}={\overline{y}}_i{}^{\left(ru\text{-ka}\right)}+m_i{}^{\left(ru\text{-ka}\right)}\cdot h$

Die Berechnungsergebnisse für beide Verfahren sowie die Werte $y_i$ der exakten Lösung sind in folgender Tabelle enthalten.

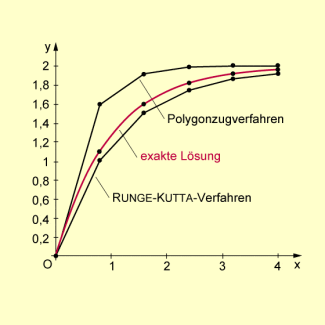
Sowohl die Tabelle als auch die grafische Darstellung deuten an, dass im Allgemeinen numerische Lösungen nach dem RUNGE-KUTTA-Verfahren kleinere Abweichungen gegenüber der exakten Lösung aufweisen als numerische Lösungen nach dem Polygonzugverfahren.