Richtungsfeld einer Differenzialgleichung

Gewöhnliche Differenzialgleichungen beschreiben Kurvenscharen in der Ebene. Eine Differenzialgleichung 1. Ordnung ordnet jedem Punkt der xy-Ebene einen Wert zu (vorausgesetzt, dass für den Punkt ein Wert definiert ist), welcher der Richtung der Tangente der Integralkurve in diesem Punkt entspricht, ein sogenanntes Linienelement.
Die Gesamtheit der Linienelemente ist das durch die Differenzialgleichung beschriebene Richtungsfeld. Das Bestimmen der Lösung der Differenzialgleichung ist das Bestimmen der Kurven, die auf dieses Richtungsfeld „passen“.

KI-Tutor Kim erklärt dir den Stoff sofort nochmal einfach und verständlich
Kim hilft dir bei all deinen Fragen und Aufgaben weiter

Jetzt kostenlos mit Kim üben

Durch die explizite Differenzialgleichung 1. Ordnung $y^{'} = f (x, y)$ sei für jeden Punkt $P (x_{0}; y_{0})$ ein Wert definiert, nämlich $f (x_{0}; y_{0})$ , er beschreibt den Anstieg der Integralkurve in diesem Punkt: $y^{'} (x_{0}; y_{0}) = f (x_{0}; y_{0})$
Durch $y^{'} = c o n s t .$ werden Kurven mit gleichen Linienelementen (oder Richtungselementen) beschrieben, sogenannte Isoklinen oder Neigungslinien.

Beispiel: Die Differenzialgleichung $(2 y - x^{2}) d x + d y = 0$ lautet in expliziter Darstellung $y^{'} = x^{2} - 2 y$ .
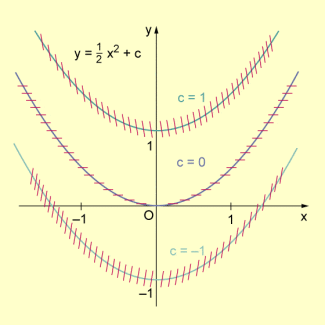
Isoklinen ergeben sich für $y^{'} = c_{1}, a l s o x^{2} - 2 y = c_{1}$ . Das sind die Parabeln $y = \frac{1}{2} x^{2} + c$ , also gestauchte, nach oben geöffnete Parabeln symmetrisch zur y-Achse.

Die Isoklinen von $y y^{'} - x = 0$ ergeben sich $\frac{x}{y} = c, y \neq 0, a l s o y = \frac{x}{c}$ .
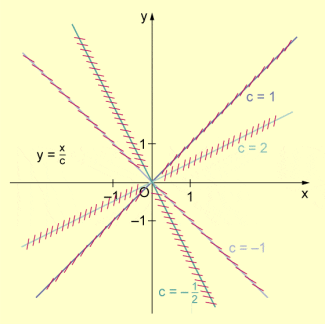
Die Isoklinen sind Halbgeraden.

$y' = - \frac{1}{4} \frac{x}{y}, y \neq 0,$ soll im 1. Quadraten betrachtet werden.
Die Isoklinen sind $y = - \frac{1}{4 c} x$ .

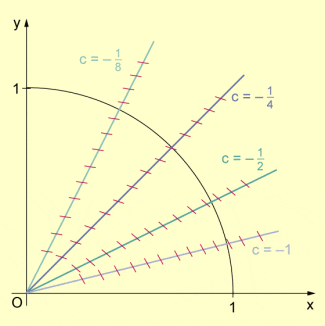
Eine grobe Näherung für die Integralkurve erhielte man, wenn man einen Polygonzug dem Richtungsfeld anpasst.

Lernhelfer (Duden Learnattack GmbH): "Richtungsfeld einer Differenzialgleichung ." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/richtungsfeld-einer-differenzialgleichung (Abgerufen: 21. May 2026, 06:44 UTC)

Suche nach passenden Schlagwörtern

Jetzt mit Kim üben

KI-Tutor Kim erklärt dir den Stoff sofort nochmal einfach und verständlich
Kim hilft dir bei all deinen Fragen und Aufgaben weiter

Verwandte Artikel

Das Runge-Kutta-Verfahren

Soll eine explizite Differenzialgleichung $f' (x) = G (x; f (x))$ mit der Anfangsbedingung $f (x_{0}) = y_{0}$ numerisch nach dem Polygonzugverfahren gelöst werden, so benutzt man die Differenzengleichung $\bar{f} (x + h) = \bar{f} (x) + h \cdot G (x; \bar{f} (x))$ .

Dabei ist $\bar{y} = \bar{f} (x)$ eine Näherung für die eigentlich gesuchte Funktion $y = f (x) .$

Bei Übergang zur Darstellung der Differenzengleichung als iterative Bildungsvorschrift ergibt sich ${\bar{y}}_{i + 1} = {\bar{y}}_{i} + h \cdot G (x_{i}; {\bar{y}}_{i})$ bzw. ${\bar{y}}_{i + 1} = {\bar{y}}_{i} + h \cdot m_{i}^{(p o l y)} {mit m}_{i}^{(p o l y)} = G (x_{i}; {\bar{y}}_{i})$ .

Darstellung geometrischer Objekte durch Differenzialgleichungen

Die Lösungen (Integrale) von Differenzialgleichungen sind Kurvenscharen. Entsprechend lassen sich Klassen von Kurven, die sich nur durch konstante Parameter unterscheiden, durch Differenzialgleichungen darstellen. Im Folgenden werden Differenzialgleichungen für geometrische Grundgebilde wie Gerade, Kreis, Parabel, Ellipse und Hyperbel angegeben.

Differenzialgleichungen zur Beschreibung von Federschwingungen

Ein Körper, der an einer Feder befestigt ist, führt nach einer Auslenkung eine Schwingung durch. Der Ort des Körpers wird durch die zeitabhängige Ortskoordinate y(t) beschrieben, deren Gleichung gefunden werden soll.
Im Folgenden werden mit einer derartigen Anordnung gedämpfte und ungedämpfte Schwingungen untersucht.

Differenzialgleichungen zur Beschreibung des Lade- und Entladevorgangs eines Kondensators

In einem Gleichstromkreis befindet sich eine Spannungsquelle mit der Spannung $U_{0}$ ein ohmscher Widerstand R und ein Kondensator mit der Kapazität C.
Wird Spannung angelegt, so fließt über den Widerstand R ein Strom I zum Kondensator und lädt ihn auf. Dabei wächst die Kondensatorspannung $U_{C} = \frac{Q}{C} .$

Beim Stromfluss fällt am Widerstand die Spannung $U_{R} = I \cdot R$ ab. Die Summe aus Spannungsabfall am ohmschen Widerstand und Kondensatorspannung ist immer gleich der Spannung der Spannungsquelle.

Es gilt also $U_{0} = U_{R} + U_{C} = I R + \frac{Q}{C},$ woraus mit $I = \frac{d Q}{d t}$ folgt:
$U_{0} = R \frac{d Q}{d t} + \frac{Q}{C} b z w . \frac{d Q}{d t} + \frac{Q}{R C} = \frac{U_{0}}{R}$

Diese Gleichung ist eine lineare inhomogene Differenzialgleichung 1. Ordnung der Form $f' (x) + q f (x) = s$ mit den Koeffizienten $q = \frac{1}{R C} u n d s = \frac{U_{0}}{R}$ sowie der gesuchten Funktion $Q = Q (t)$ , die im Folgenden zu lösen ist.

Differenzialgleichungen zur Beschreibung der Füllstandssteuerung einer Talsperre

Der Füllstand einer Talsperre wird ausgedrückt durch das (aktuelle) Stauvolumen V(t), das sich durch den Zu- und Abfluss von Wasser mit der Zeit t ändern kann. Zu- und Abfluss von Wasser geben an, welches Wasservolumen pro Zeiteinheit in die Talsperre hinein- bzw. aus ihr herausfließt.
Beide werden zusammengefasst zur Wasserzufuhr Z(t), die sich ebenfalls mit der Zeit ändern kann. Überwiegt der Zufluss, so gilt $Z (t) \geq 0,$ überwiegt dagegen der Abfluss, so ist $Z (t) \leq 0$ .

Richtungsfeld einer Differenzialgleichung

Thema nicht verstanden?

Suche nach passenden Schlagwörtern