Direkter Beweis

Prozess der Beweisfindung

Wir betrachten den Prozess der Beweisfindung an einem Beispiel und wählen dazu den folgenden Sachverhalt aus:

• Beispiel 1: Die Summe von Primzahlzwillingen $pundp+2(mitp\ge 5)$ ist stets durch 12 teilbar.

(1) Aufbau eines Suchfeldes

Analyse des Sachverhalts
Die „Wenn, dann“-Form des Satzes lautet: Wenn z die Summe von Primzahlzwillingen ist, so gilt $12|z$. Damit lassen sich die Voraussetzung ($p,p+2\in P;p\ge 5$ ) und die Behauptung ($12|z$ ) ablesen.

Der Satz stellt eine Allaussage dar, von der noch nicht feststeht, ob sie wahr oder falsch ist. Eine Allaussage widerlegt man durch Angabe eines Gegenbeispiels; ihre Wahrheit zeigt man durch einen Beweis.

Betrachten von Beispielen
$\begin{array}{l}5+7=1229+31=60\\ 11+13=2441+43=84\\ 17+19=36\mathrm{...}\end{array}$
In jedem dieser Beispiele ist die Summe in der Tat durch 12 teilbar.

Umstrukturierung des Wissensspeichers
Was ist eine Primzahl? Eine Primzahl ist eine natürliche Zahl (größer als 1), die nur durch 1 und sich selbst teilbar ist. 0 und 1 sind weder Primzahlen noch zusammengesetzte Zahlen. Die kleinste (und einzige gerade) Primzahl ist die 2. Primzahlzwillinge sind Primzahlen, die sich um 2 unterscheiden.
Wann ist eine Zahl durch 12 teilbar? Wenn eine Zahl durch 3 und durch 4 teilbar ist, so ist diese Zahl auch durch 12 teilbar.

(2) Bearbeitung des Suchfeldes (Finden einer Beweisidee)

Beim Suchen von Beweisideen können zwei Strategien helfen: das sogenannte Vorwärtsarbeiten und das sogenannte Rückwärtsarbeiten.

Beim Vorwärtsarbeiten geht man von den gegebenen Voraussetzungen aus und stellt sich eine Reihe typischer Fragen wie etwa die folgenden:

• Was ist bekannt? Was weiß man über die Figur?
• Wie kann man das Bekannte mathematisch erfassen und aufschreiben?
• Was folgt aus den Voraussetzungen?
• Welche Sätze mit gleichen oder ähnlichen Voraussetzungen sind bekannt?

Beim Rückwärtsarbeiten geht man von der zu beweisenden Behauptung aus. Typische Fragen bei diesem Vorgehen sind:

• Wie heißt die Behauptung?
• Kennt man Sätze mit gleicher oder ähnlicher Behauptung?
• Welche dieser Sätze haben die gleichen Voraussetzungen wie der behauptete Satz oder lassen sich solche Voraussetzungen schaffen?

Für unser anstehendes Beweisproblem scheint das Vorwärtsarbeiten günstig zu sein: In Auswertung der Voraussetzungen ist zu zeigen, dass 3 Teiler der Summe ist und dass 4 Teiler der Summe ist. Daraus würde die Behauptung folgen.

(3) Durchführung des Beweises

1. Voraussetzung:
   $p,p+2\in P;p+\left(p+2\right)=z$
2. Behauptung:
   $12|z$
3. Beweis:

Ausgehend von dem betrachteten Beispiel lässt sich die Struktur des direkten Beweises abheben:
Aus der Voraussetzung des Satzes sowie bereits bekannten Tatsachen (Definitionen, Lehrsätze) wird mithilfe einer endlichen Anzahl gültiger Schlussregeln direkt die Wahrheit der Behauptung gezeigt.

Beweisführung mittels Rückwärtsarbeitens

Im Folgenden soll auch das Rückwärtsarbeiten beim Beweisen demonstriert werden. Dazu betrachten wir den folgenden Satz:

• Beispiel 2: Wenn ABCD ein Sehnenviereck ist, so ist die Summe der Gegenwinkel $180°$.

1. Voraussetzung:
   ABCD ist Sehnenviereck.
2. Behauptung:
   $\begin{array}{l}\alpha +\gamma =180°\\ \beta +\delta =180° \end{array}$

Das Rückwärtsarbeiten fragt nach Sätzen mit gleicher oder ähnlicher Behauptung (hier: Winkelsumme von $180°$).

Welche Sätze sind also bekannt, die etwas über Winkel und Winkelsummen, die $180°$ betragen, aussagen? In Beantwortung der Frage entsteht etwa folgender umstrukturierter Wissensspeicher:

• Innenwinkelsatz für Dreiecke ($\alpha +\beta +\gamma =180°$)
• Nebenwinkelsatz ($\alpha +\beta =180°$)
• Innenwinkelsatz für Vierecke ($\alpha +\beta +\gamma +\delta =360°$)
• Entgegengesetzt liegende Winkel an geschnittenen Parallelen ergänzen sich zu $180°$.
• Bestimmte Nachbarwinkelpaare im Parallelogramm ergänzen sich zu $180°$.
• Bestimmte Nachbarwinkelpaare im Trapez ergänzen sich zu $180°$.

Welche dieser Sätze lassen sich anwenden? Der zweite, vierte, fünfte und sechste Satz entfallen sofort, da deren Voraussetzungen mit denen unseres zu beweisenden Satzes nicht vereinbar sind. Bleiben also der erste und der dritte Satz, wobei der Innenwinkelsatz für Dreiecke den größten Bezug aufweist.

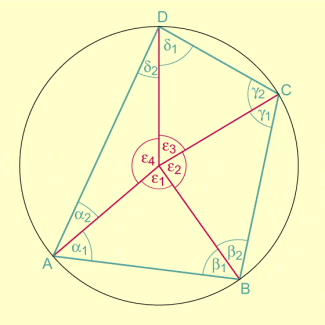
In der Figur sind zwar keine Dreiecke vorhanden, doch durch Einzeichnen von Hilfslinien lassen sich welche erzeugen. Als Möglichkeiten bieten sich an (siehe Bild):
(1) Einzeichnen der Diagonalen
(2) Einzeichnen der Radien vom Mittelpunkt M zu den Eckpunkten des Sehnenvierecks

Im ersten Fall sind beliebige Dreiecke, im zweiten gleichschenklige Dreiecke (mit jeweils gleich großen Basiswinkeln) entstanden. Im zweiten Fall lässt sich die Idee, den Innenwinkelsatz für Dreiecke anzuwenden, nutzbringend realisieren.

3. Beweis:

Ziel ist zu zeigen, dass $\alpha +\gamma =180°$ gilt. Aufschreiben der Innenwinkelbeziehungen (anhand der Bezeichnungen im Bild) für die vier Teildreiecke bei gleichzeitigem Ersetzen der Teilwinkel von $\beta$ und $\delta$ durch die entsprechenden Teilwinkel von $\alpha$ und $\gamma$ ergibt:
$\begin{array}{l}2{\alpha }_1+{\epsilon }_1=180°\\ 2{\gamma }_1+{\epsilon }_2=180°\\ 2{\gamma }_2+{\epsilon }_3=180°\\ 2{\alpha }_2+{\epsilon }_4=180°\end{array}$

Addition dieser Gleichungen ergibt
$2{\alpha }_1+2{\alpha }_2+2{\gamma }_1+2{\gamma }_2=360°$

und weiter
$({\alpha }_1+{\alpha }_2)+({\gamma }_1+{\gamma }_2)=\alpha +\gamma =180°$.

Analog folgt
$\beta +\delta =180°$.

Anmerkung: Ein Vorteil des Rückwärtsarbeitens besteht insbesondere in der Erschließung notwendiger Hilfslinien.