Direkt zum Inhalt

Beweise unter Verwendung von Vektoren

Sätze der ebenen Geometrie lassen sich mithilfe von Vektoren mitunter sehr knapp und übersichtlich beweisen. Auf der Grundlage entsprechender Figuren, in denen die relevanten Stücke vektoriell gekennzeichnet werden, formuliert man Voraussetzungen und Behauptung jeweils mittels Vektoren und versucht, durch logische Schlüsse unter Verwendung der Rechengesetze für Vektoren den Beweis zu führen.
Bereits Addition und Vervielfachung von Vektoren können dabei sehr hilfreich sein, die Hinzunahme multiplikativer Verknüpfungen und deren Eigenschaften erschließen weitere Anwendungsmöglichkeiten. Die folgenden Beispiele illustrieren diese Vorgehensweise.

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

  • Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
  • 24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
  • Viel günstiger als andere Nachhilfe und schützt deine Daten.
Jetzt 30 Tage risikofrei testen

Beispiel 1: Man beweise: In einem Dreieck ist die Verbindungsstrecke zweier Seitenmittelpunkte parallel zur dritten Seite und halb so lang wie diese.

  • Dreieck / Verbindungsstrecke von Seitenmittelpunkten

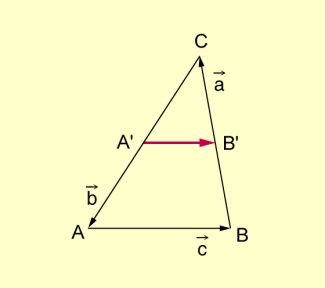
Voraussetzung:
a → + b → + c → = o →   ;         B   B ' → = B '   C → = 1 2   a →   ;             C   A ' → = A '   A → = 1 2   b →

Behauptung:
A '   B ' → = 1 2   c →

Beweis:
A '   B ' → = − 1 2   b → + ( − 1 2   a → ) = − 1 2 (   b → + a ¯   ) = − 1 2 (   a → + b ¯   )
Mit a → + b → = −   c → folgt A '   B ' → = − 1 2   ( −   c → ) = 1 2   c → .
w.z.b.w.

Beispiel 2: Es ist zu beweisen, dass in einem Trapez die Mittellinie (also die Verbindungsstrecke der Schenkelmittelpunkte) parallel zu den Grundseiten verläuft und halb so lang wie deren Summe ist.

  • Mittellinie im Trapez

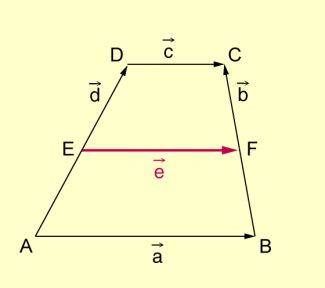
Voraussetzung:
a → + b → − c → − d → = o →   ;         a →   | |   c → ;           A   E → = 1 2   d → ;           B   F → = 1 2   b →

Behauptung:
e → = 1 2   (   a → + c →   )

Beweis:
a → + 1 2     b → − e → − 1 2     d → = o →   ;         e → + 1 2     b → − c →     − 1 2     d → = o →

Löst man beide Gleichungen nach e → auf, so folgt:
e → = a → + 1 2     b → − 1 2     d →             b z w .             e → = c → + 1 2     d → − 1 2     b →

Durch Addition dieser beiden Gleichungen und Division durch 2 erhält man schließlich:
e → = 1 2   (   a → + c →   )
w.z.b.w.

Beispiel 3: Es ist nachzuweisen, dass die Seitenhalbierenden eines Dreiecks ABC einander in einem Punkt S schneiden und dass dieser Schnittpunkt (der Schwerpunkt des Dreiecks genannt wird) jede Seitenhalbierende im Verhältnis 2       :       1 teilt. Man zeige hierzu, dass s → = 1 3   (   a → + b → + c →   ) für die Ortsvektoren der Punkte S, A, B bzw. C gilt.

  • Schnittpunkt der Seitenhalbierenden eines Dreiecks

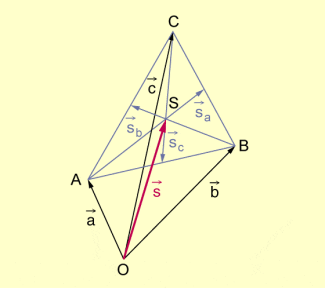
Nachweis:
Wir vergleichen a → + 2 3   s → a   ,         b → + 2 3   s → b           u n d           c → + 2 3   s → c als Ortsvektoren bezüglich O.
Mit   s → a = 1 2   (   b → + c →   ) − a → gilt:
a → + 2 3   s → a = 2 3 (   1 2   (   b → + c →   ) − a → ) = 1 3   (   a → + b → + c →   )
Ebenso erhält man:
b → + 2 3   s → b = 1 3   (   a → + b → + c →   )               u n d           c → + 2 3   s → c = 1 3   (   a → + b → + c →   )
Alle drei zu vergleichenden Ortsvektoren beschreiben also den Schnittpunkt S der Seitenhalbierenden eines Dreiecks ABC: O   S → = s → = 1 3   (   a → + b → + c →   )     .
Dieser Punkt S teilt jede Seitenhalbierende im Verhältnis 2       :       1 .

Verwendet man außer Addition und Vervielfachung von Vektoren auch noch multiplikative Verknüpfungen und deren Eigenschaften, so ergeben sich weitere Anwendungsmöglichkeiten.

Beispiel 4: Man beweise den Satz des THALES auf vektoriellem Wege.

  • Winkel im Halbkreis

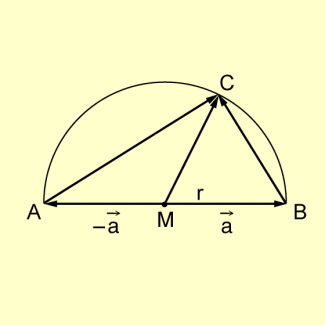
Voraussetzung:
A   M ¯ = M   B ¯ = |   a →   |   = r ;         M   C ¯ = |   b →   | = r    

Behauptung:
∢     B   C   A = 90 °  

Beweis:
A   C →     ⋅     B   C →   = (   a → + b →   ) ⋅ (   b → − a →   ) = −   a → 2 + b → 2
Wegen |   a →   |   = |   b →   | = r   ,       a l s o       a → 2 = b → 2 , gilt damit A   C →     ⋅     B   C →   = 0 , d.h.: AC → ⊥ BC →
Damit folgt ∢     B   C   A = 90 °   .
w.z.b.w.

Lernhelfer (Duden Learnattack GmbH): "Beweise unter Verwendung von Vektoren." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/beweise-unter-verwendung-von-vektoren (Abgerufen: 20. May 2025, 00:13 UTC)

Suche nach passenden Schlagwörtern