Galton-Brett
BERNOULLI-Ketten und damit binomialverteilte Zufallsgrößen lassen sich mit einem GALTON-Brett veranschaulichen.
Das GALTON-Brett besteht aus einem geneigt aufgestellten Brett, in dem in regelmäßigen Horizontalreihen Stifte angebracht sind und zwar in aufeinanderfolgenden Reihen auf Lücke gesetzt. Lässt man nun aus einem oben in der Mitte angebrachten Trichter Kugeln passender Größe (mit einem Durchmesser wenig kleiner als der freie Abstand zwischen zwei benachbarten Stiften) über dieses Brett rollen, so werden sie infolge der Zusammenstöße mit den Stiften aus ihrer Bahn (entsprechend der Erdanziehung auf der „schiefen Ebene“) in unregelmäßiger Weise nach rechts oder links (aus Sicht der rollenden Kugel) abgelenkt und sammeln sich unterhalb der Stiftreihen in verschiedenen, nebeneinander angeordneten Fächern. Diese Fächer sind von links nach rechts mit den Zahlen von 0 bis n durchnummeriert. Die folgende Abbildung zeigt ein vierreihiges GALTON-Brett mit fünf Fächern.
Vierreihiges Galton-Brett
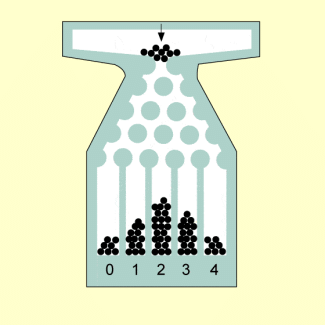
Soll das GALTON-Brett für mathematische Betrachtungen genutzt werden, muss gewährleistet sein, dass das Hinabrollen der Kugel ein „rein zufälliger“ Vorgang ist. Das erfordert einige Modellannahmen wie die folgenden:
- vollständige Glattheit der geneigten Ebene;
- exakte Anordnung der Stifte;
- exakte Kugelgestalt der rollenden Kugeln, Kugeldurchmesser fast genau gleich dem freien Abstand der Stifte;
- völlig unelastische Stöße zwischen Kugeln und Stiften
Die zufällige Anzahl der Kugeln in den einzelnen Fächern ist unter diesen Modellannahmen binomialverteilt mit den Parametern n und .
Die Wahrscheinlichkeit, dass eine Kugel im Fach k aufgefangen wird, beträgt:
Beschriftet man den i-ten Zapfen in der k-ten Reihe des GALTON-Brettes mit
,
d.h. mit der Anzahl der Wege, die zu ihm führen, so erhält man das pascalsche Dreieck, wobei der Trichter mit
bezeichnet wird.
Durch eine zusätzliche seitliche Neigung des GALTON-Brettes könnte auch der Fall anderer Werte für p verwirklicht werden.
Reale GALTON-Bretter weichen von den obigen idealen Modellbedingungen ab, sodass sich die Kugeln in den Fächern nur angenähert binomialverteilt häufen.
Die heutigen technischen Möglichkeiten einer virtuellen Simulation auf der Grundlage von Pseudozufallszahlen gestatten es, den obigen Modellannahmen wesentlich besser zu entsprechen als eine Konstruktion aus Holz und Stahl.
Mit dem GALTON-Brett kann experimentell die Approximation der Binomialverteilung durch die Normalverteilung (Grenzwertsatz von MOIVRE-LAPLACE) bestätigt werden. Es ermöglicht auch die Illustration einiger grundsätzlicher physikalischer Erscheinungen der Diffusion und der Wärmeleitung wie z.B. der brownschen Molekularbewegung und der Diffusion zweier Gase entsprechend den loschmidtschen Versuchen.
Der Name GALTON-Brett geht auf den englischen Naturforscher FRANCIS GALTON (1822 bis 1911) zurück. Er war ein Cousin von CHARLES DARWIN. So ist es in gewissem Sinne nahe liegend, dass er sich wissenschaftlich hauptsächlich mit den Erscheinungen der Vererbung beschäftigte. In diesem Zusammenhang entwickelte er Ideen für eine messende Statistik, insbesondere die Begriffe Regression und Korrelation.
GALTON war ein reicher Mann. Sein Vermögen gestattete es ihm, eine umfangreiche Expedition nach Südwestafrika (1850 bis 1862) durchzuführen, mit der er sich einen Namen als Entdeckungsreisender machte. Seit 1860 war GALTON Fellow der Royal Society.
Korrelation Darwin binomialverteilte Zufallsgrößen Moivre Normalverteilung pascalsches Dreieck Grenzwertsatz Laplace Approximation Bernoulli-Ketten Pseudozufallszahlen virtuelle Simulation Binomialverteilung Animation Regression
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 