Kugel und Tangentialebene

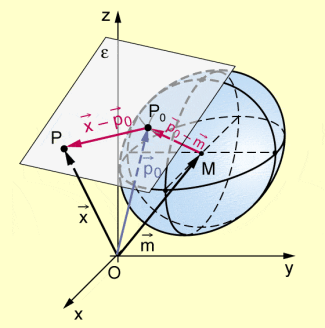
Der Vektor $\overrightarrow{M{P}_0}$ ist folglich Normalenvektor der Tangentialebene.
Es gilt (mit P als beliebigem Punkt der Tangentialebene):
$\overrightarrow{P{P}_0}\cdot \overrightarrow{M{P}_0}=0$
Somit hat man eine vektorielle Gleichung der Tangentialebene:
$\left(\overrightarrow{x}-\overrightarrow{p_0}\right)\cdot \left(\overrightarrow{p_0}-\overrightarrow{m}\right)=0$
Man kann die Tangentialebene aber auch durch eine Gleichung in Koordinatenform beschreiben.
Diese erhält man ganz einfach aus der Kugelgleichung ${\left|\overrightarrow{x}-\overrightarrow{m}\right|}^2=r^2,$ indem man einmal den Vektor $\overrightarrow{x}$ durch den Ortsvektor zum Berührungspunkt $P_0$ ersetzt:
$\begin{array}{l}\left(\overrightarrow{x}-\overrightarrow{m}\right)\cdot \left(\overrightarrow{p_0}-\overrightarrow{m}\right)=r^2\\ \left(x-c\right)\left(x_0-c\right)+\left(y-d\right)\left(y_0-d\right)+\left(z-e\right)\left(z_0-e\right)=r^2\end{array}$

Will man für einen Punkt $P_0\left(x_0;y_0;z_0\right)$ einer Kugel die Gleichung der Tangentialebene finden, so setzt man die entsprechenden Werte in die oben genannten Gleichungen ein.

• Beispiel 1: Eine Kugel k sei gegeben durch M(–1; 4; 0) und r = 3.
  Die Gleichung der Tangentialebene im Punkt $P_0\left(0;2;-2\right)$ ist zu ermitteln.

Die Gleichung der Kugel lautet ${\left(x+1\right)}^2+{\left(y-4\right)}^2+z^2=9.$
Jeder Punkt P der Tangentialebene mit dem Ortsvektor $\overrightarrow{x}$ muss dann die folgende Gleichung erfüllen:
$\overrightarrow{P{P}_0}\cdot \overrightarrow{M{P}_0}=0bzw.\left[\overrightarrow{x}-\left(\begin{array}{c}0\\ 2\\ -2\end{array}\right)\right]\cdot \left(\begin{array}{c}1\\ -2\\ -2\end{array}\right)=0$
Durch Einsetzen ergibt sich nun:
$1\cdot \left(x+1\right)-2\cdot \left(y-4\right)-2\cdot z=9bzw.x-2y-2z=0$

Will man dagegen feststellen, ob eine bestimmte Ebene $\epsilon$ Tangentialebene einer Kugel ist, so untersucht man, ob es einen Berührungspunkt $P_0$ gibt.

• Beispiel 2: Eine Ebene $\epsilon$ sei gegeben durch $x-2y+2z=15$ und eine Kugel k durch $M\left(2;1;3\right)undr=3$ bzw. die Gleichung ${\left(x-2\right)}^2+{\left(y-1\right)}^2+{\left(z-3\right)}^2=9.$
  Es ist zu prüfen, ob $\epsilon$ eine Tangentialebene von k ist.

Der Abstand der Ebene vom Mittelpunkt M der Kugel wird folgendermaßen berechnet:
$d_{M;\epsilon }=\left|\left[\left(\begin{array}{c}2\\ 1\\ 3\end{array}\right)-\left(\begin{array}{c}3\\ 1\\ 7\end{array}\right)\right]\cdot \left(\begin{array}{c}1\\ -2\\ 2\end{array}\right)\cdot \frac{1}{3}\right|=\left|\frac{-1-8}{3}\right|=3$
Damit ist $d_{M;\epsilon }=r=3$, sodass $\epsilon$ die Kugel k berührt und damit eine Tangentialebene von k ist.

Ermitteln des Berührungspunktes:
Die senkrecht auf $\epsilon$ stehende durch M verlaufende Gerade $g_{M\perp \epsilon }=g$ hat die folgende Punktrichtungsgleichung:
$g\text{:}\overrightarrow{x}=\left(\begin{array}{c}2\\ 1\\ 3\end{array}\right)+t\left(\begin{array}{c}1\\ -2\\ 2\end{array}\right)\left(t\in ℝ\right)$
Für den Schnittpunkt von g und $\epsilon$ ergibt sich dann:
$\begin{array}{c}\left(2+t\right)-2\left(1-2t\right)+2\left(3+2t\right)=15\\ 9t=9\\ t=1\end{array}$
Damit hat der Berührungspunkt $P_0$ die Darstellung $P_0\left(3;-1;5\right)$.
Probemöglichkeit:
$\overrightarrow{M{P}_0}=\left(\begin{array}{c}1\\ -2\\ 2\end{array}\right)=\overrightarrow{n_{\epsilon }}$
$\overrightarrow{M{P}_0}$ ist ein Normalenvektor von $\epsilon$, was eine notwendige Bedingung dafür ist, dass $\epsilon$ eine Tangentialebene von k ist.