Kugel und Tangentialkegel
Durch einen beliebigen Punkt P außerhalb einer Kugel k lassen sich unendlich viele Geraden so legen, dass jede von ihnen eine Tangente der Kugel k ist.
Diese Geraden – also die Tangenten – bilden einen (doppelten) Kreiskegel, den Tangentialkegel der Kugel k mit der Spitze P.
Die Berührungspunkte aller Tangenten, die einen Tangentialkegel bilden, liegen auf einem Kreis, also in einer Ebene.
-
Tangentialkegel der Kugel
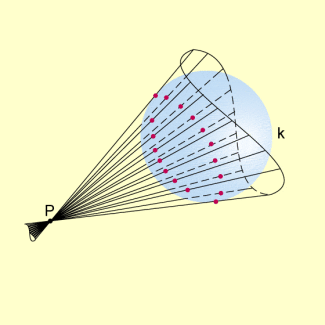
Die Gleichung dieser Ebene lässt sich wie folgt ermitteln
(siehe dazu die folgende Abbildung):
![]()
Alle Berührungspunkte müssen demzufolge die Gleichung erfüllen, wobei der Ortsvektor des Mittelpunktes der Kugel k, der Ortsvektor der Spitze des Tangentialkegels P und der Ortsvektor des Berührungspunktes ist.
Der Schnittkreis dieser Ebene mit der Kugel ist der Kreis, auf dem alle Berührungspunkte des Tangentialkegels mit der Spitze P an die Kugel k liegen.
Die Koordinaten des Mittelpunktes und des Radius dieses Berührungskreises ermittelt man also wie die des Schnittkreises einer Ebene mit einer Kugel.
- Beispiel: Es ist der Berührungskreis des Tangentialkegels mit der Spitze an die Kugel k mit und zu ermitteln.
Die Ebene der Berührungspunkte ist durch die folgenden Gleichungen gegeben:
Die durch M in Richtung
verlaufende Gerade hat dann die Punktrichtungsgleichung
Ermitteln des Mittelpunktes des Schnittkreises
Daraus ergibt sich der Mittelpunkt
Ermitteln des Abstandes d des Mittelpunktes M von der Ebene
Als Radius des Berührungskreises ergibt sich dann:

