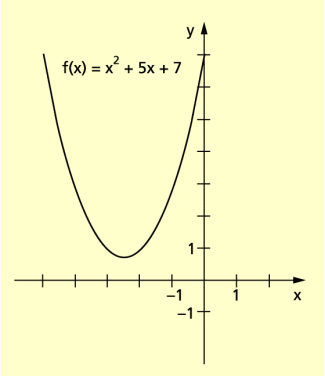
Quadratische Funktionen

Nimmt man vereinfachend an, dass ein Bungee-Springer in der ersten Phase nach seinem Absprung aus $h_0$ Meter Höhe frei fällt, so würde er sich entsprechend den Gesetzen der Physik nach t Sekunden in einer Höhe
$h=h_0-\frac{g}{2}\cdot t^2\left(g=\mathrm{9,81}\frac{m}{s^2}\right)$
über der Erdoberfläche befinden.

Die Gleichung
$h\left(t\right)=h_0-\frac{g}{2}\cdot t^2$
beschreibt eine spezielle quadratische Funktion.

• Definition: Eine Funktion mit einer Gleichung der Form
  $y=f\left(x\right)=a{x}^2+bx+c(\text{mit }a\ne \mathrm{0,}x\in ℝ)$
  oder einer Gleichung, die durch äquivalentes Umformen in diese Form überführt werden kann, heißt quadratische Funktion
  ($a{x}^2$ nennt man das quadratische Glied, bx das lineare Glied und c das absolute Glied der Funktionsgleichung).

Der Graph einer quadratischen Funktion ist eine Parabel (quadratische Parabel). Die Symmetrieachse der Parabel verläuft parallel zur y-Achse und schneidet den Graphen der Funktion im Scheitelpunkt (Scheitel) der Parabel.
Für a > 0 ist die Parabel nach oben und für a < 0 nach unten geöffnet.

Für a > 0 besitzt die Parabel einen tiefsten Punkt (einen Minimumpunkt) und für a < 0 einen höchsten Punkt (einen Maximumpunkt). Diese Punkte sind jeweils Scheitelpunkt der Parabel.

Wir betrachten zunächst quadratische Funktionen mit a = 1. Man erhält
$y=f\left(x\right)=x^2+bx+c$
bzw. durch Umbenennung
$y=f\left(x\right)=x^2+px+q(mitp,q\in ℝ)$
Um den Zusammenhang zwischen den reellen Zahlen p, q und den Graphen der entsprechenden quadratischen Funktionen zu erkennen, ist es zweckmäßig, eine Fallunterscheidung durchzuführen.

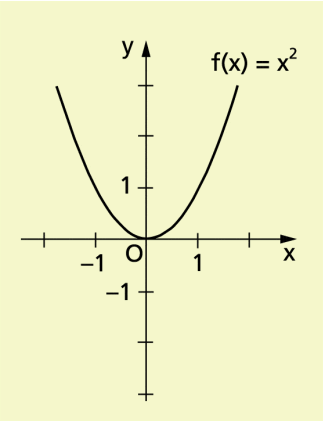
Fall 1: p = 0, q = 0
Man erhält die quadratische Funktion $f\left(x\right)=x^2$.
Ihr Definitionsbereich ist die Menge der reellen Zahlen, ihr Wertebereich die Menge aller nichtnegativen reellen Zahlen.
Der Graph dieser Funktion wird Normalparabel genannt.
Ihre Symmetrieachse ist die y-Achse; der Scheitel hat die Koordinaten (0; 0).
Aufgrund der im Funktionsterm auszuführenden Operation (Quadrieren) ist die Funktion $f\left(x\right)=x^2$ für alle $x\le 0$ streng monoton fallend und für alle $x\ge 0$ streng monoton wachsend sowie nach unten beschränkt.

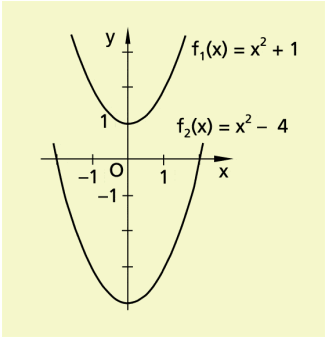
Fall 2: p = 0; q $\ne$0
Es ergibt sich die Gleichung $f\left(x\right)=x^2+q$ mit $q\in ℝ$, z.B. also
$y=f_1\left(x\right)=x^2+1$ oder $y=f_2\left(x\right)=x^2-4$.
Im Vergleich zum zuvor betrachteten Fall erhält man die Funktionswerte der jeweiligen Funktion, indem man zum entsprechenden Funktionswert von $f\left(x\right)=x^2$ die Zahl 1 addiert bzw. von diesem 4 subtrahiert (allgemein: q addiert).
Das heißt geometrisch: Der Graph der Funktionen $f\left(x\right)=x^2+q$ ist eine um $\left|q\right|$ Einheiten in Richtung der positiven (für q > 0) bzw. negativen y-Achse (für q < 0) verschobene Normalparabel mit der y-Achse als Symmetrieachse und dem Scheitel (0; q).

Fall 3: p ≠  0, q = 0
Man erhält die Gleichung $f\left(x\right)=x^2+px$ mit $p\in ℝ$, zum Beispiel also
$y=f\left(x\right)=x^2+2x$.

Um mit den vorangegangenen Fällen vergleichen zu können, liegt es nahe, die Summe im Funktionsterm in ein vollständiges Quadrat umzuwandeln.
Das ist mithilfe der quadratischen Ergänzung möglich:
$f\left(x\right)=x^2+2x+1-1={\left(x+1\right)}^2-1$
Die Funktionsgleichung erreicht damit die Gestalt $f\left(x\right)={\left(x+d\right)}^2+e$.
Der Einfluss des Summanden e auf den Graphen der Funktion ist bekannt (siehe Fall 2).
Anhand der Funktionsgleichungen $h\left(x\right)=x^2$ und $f\left(x\right)={\left(x+d\right)}^2$erkennt man:
Der Funktionswert, den die Funktion $h\left(x\right)=x^2$ an einer beliebigen Stelle x annimmt, ist gleich dem Funktionswert von
$f\left(x\right)={\left(x+d\right)}^2$ an der Stelle x – d, denn
$f\left(x-d\right)={\left[\left(x-d\right)+d\right]}^2=x^2=h\left(x\right)$.
Also: Der Graph der Funktion y = $f\left(x\right)={\left(x+d\right)}^2$ ist die um $\left|d\right|$Einheiten in Richtung der positiven (falls d < 0) oder der negativen x-Achse (falls d > 0) verschobene Normalparabel.
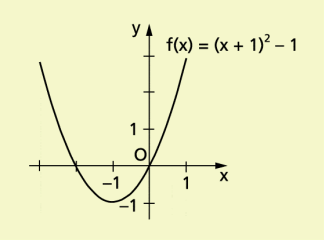
In Bezug auf das betrachtete Beispiel $y=f\left(x\right)=x^2+2x$ bzw. $y=f\left(x\right)={\left(x+1\right)}^2$– 1 bedeutet das: Der Graph der Funktion ist die um je eine Einheit in Richtung der negativen x- und y-Achse verschobene Normalparabel; der Scheitelpunkt ist S(–1; –1).

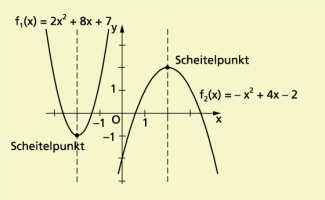
Fall 4: p $\ne$0; q $\ne$0
Man erhält die Gleichung $y=f\left(x\right)=x^2+px+q$ mit $p,q\in ℝ$.
Mithilfe der quadratischen Ergänzung kann diese wieder in die Struktur $y=f\left(x\right)={\left(x+d\right)}^2+e$ überführt werden, aus der sich die Koordinaten des Scheitelpunktes S(–d; e) unmittelbar ablesen lassen (siehe Fall 3).

Man spricht deshalb auch von der Scheitelpunktsform der Gleichung einer quadratischen Funktion. Bei der Umformung geht man in folgenden Schritten vor:

Das heißt: Die Koordinaten des Scheitelpunktes kann man unmittelbar aus p und q erhalten, ohne die Scheitelpunktsform zu erzeugen.
Führt man für ${\left(\frac{p}{2}\right)}^2-q=\frac{p^2}{4}-q$ die Abkürzung D ein, so erhält man für die Koordinaten des Scheitelpunktes $S\left(-\frac{p}{2};-D\right)$ bzw. $S\left(-\frac{p}{2};-\left(\frac{p^2}{4}-q\right)\right)$.
D nennt man Diskriminante der quadratischen Funktion.