Regel von Bernoulli-l'Hospital (erste Regel von l'Hospital)

Die im Folgenden betrachtete erste Regel stammt eigentlich vom Schweizer JOHANN BERNOULLI (1667 bis 1748); deswegen findet man dafür mitunter auch die Bezeichnung Regel von BERNOULLI-L'HOSPITAL.

Ausgangspunkt unserer Betrachtungen ist ein physikalisches Problem:

• In einem einfachen Gleichstromkreis mit der Spannung U befindet sich eine Spule mit dem ohmschen Widerstand R und der Induktivität (Selbstinduktion) L. Für die Stromstärke I als Funktion der Zeit t gilt dann:
  $I\left(t\right)=\frac{U}{R}\cdot \left(1-e^{-\frac{R}{L}\cdot t}\right)$
  Welche Beziehung gilt für die Stromstärke, wenn der ohmsche Widerstand R der Spule des Gleichstromkreises gleich null wäre (ideale Spule)?

Die Beantwortung dieser Frage führt zur Bildung des folgenden einseitigen Grenzwertes:
$\underset{\begin{array}{l}R\to 0\\ R>0\end{array}}{\lim I(R)}=\underset{\begin{array}{l}R\to 0\\ R>0\end{array}}{\lim }\frac{U\cdot \left(1-e^{-\frac{R}{L}\cdot t}\right)}{R}$

Fasst man nun den Zähler als Funktion u mit $u\left(R\right)=U\cdot \left(1-e^{-\frac{R}{L}t}\right)$ und den Nenner als Funktion v mit $v\left(R\right)=R$ auf, dann läge es nahe, den Grenzwertsatz für den Quotienten zweier Funktionen anzuwenden, doch dessen Voraussetzung ist wegen $\underset{\begin{array}{l}R\to 0\\ R>0\end{array}}{\lim }v\left(R\right)=0$ nicht erfüllt.

Wendet man ihn dennoch formal an, so führt das auf den unbestimmten Ausdruck $\frac{0}{0}$.

Mathematisch stößt man hier auf bestimmte Grenzen, physikalisch ist das Problem aber lösbar: Beim Schließen des Gleichstromkreises bewirkt die Selbstinduktion ein verzögertes Ansteigen des Stroms. Der Widerstand R des Stromkreises führt dazu, dass sich nach kurzer Zeit der nach dem ohmschen Gesetz geltende konstante Wert $I=\frac{U}{R}$ einstellt.

Die punktuelle Änderungsrate (Anstieg, Steigung) der Stromstärke ist durch die 1. Ableitung $I^{\prime }\left(t\right)=\frac{U}{L}\cdot e^{-\frac{R}{L}\cdot t}$ bestimmt.

Für den Einschaltmoment nimmt sie den von R unabhängigen Wert $I^{\prime }\left(0\right)=\frac{U}{L}$ an. Wäre also der Widerstand R gleich null, so würde dieser Anstieg unverändert andauern, also für die Stromstärke $I\left(t\right)$ würde gelten $I\left(t\right)=\frac{U}{L}\cdot t$.

Als (rein) mathematisches Beispiel betrachten wir das folgende:

• Es soll das Konvergenzverhalten der Funktion f mit $f\left(x\right)=\frac{x^2}{\sin x}$ an der Stelle $x_0=0$ untersucht werden.

Sowohl die Zählerfunktion $u\left(x\right)=x^2$ als auch die Nennerfunktion $v\left(x\right)=\sin x$ streben für $x\to 0$ gegen null.

Wir erhalten also wiederum einen unbestimmten Ausdruck der Form $\frac{0}{0}$.

Zerlegt man nun f in ein Produkt aus den beiden Faktoren x und $\frac{x}{\sin x}$, dann kann man mit dem Grenzwertsatz für das Produkt zweier Funktionen schlussfolgern:
$\underset{x\to 0}{\lim }\frac{x^2}{\sin x}=\underset{x\to 0}{\lim }\left(x\cdot \frac{x}{\sin x}\right)=\underset{0}{\underbrace{\underset{x\to 0}{\lim }x}}\cdot \underset{1}{\underbrace{\underset{x\to 0}{\lim }\frac{x}{\sin x}}}=0$

Mithilfe des Mittelwertsatzes der Differenzialrechnung ist es möglich, dieses Ergebnis unter anderen Gesichtspunkten zu begründen und entsprechend zu verallgemeinern. Dazu betrachten wir die Graphen von u und v.

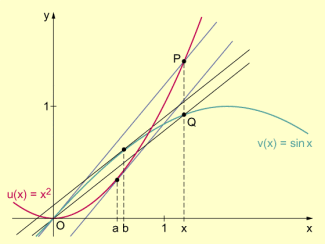
Eine Parallele zur y-Achse im Abstand $x>0$ schneidet die Graphen von u und v in den Punkten $P\left(x;u\left(x\right)\right)bzw.Q\left(x;v\left(x\right)\right)$. Verbindet man nun diese beiden Punkte mit dem Koordinatenursprung O, so sind die Geraden OP und OQ Sekanten der Graphen von u und v. Da beide Funktionen im Intervall $\left[0;x\right]$ differenzierbar sind, gibt es nach dem Mittelwertsatz im offenen Intervall $\left]0;x\right[$ mindestens zwei Stellen a und b, sodass gilt:
$\begin{array}{l}{u}^{\prime }\left(a\right)=\frac{u\left(x\right)-u\left(0\right)}{x-0}=\frac{u\left(x\right)}{x}\\ v^{\prime }\left(b\right)=\frac{v\left(x\right)-v\left(0\right)}{x-0}=\frac{v\left(x\right)}{x}\end{array}$

Somit ist $u\left(x\right)=x\cdot u^{\prime }(a)undv\left(x\right)=x\cdot v^{\prime }(b)$, und für den Grenzwert erhalten wir:
$\underset{x\to 0}{\lim }\frac{x^2}{\sin x}=\underset{x\to 0}{\lim }\frac{u\left(x\right)}{v\left(x\right)}=\underset{x\to 0}{\lim }\frac{u^{\prime }\left(a\right)\cdot x}{v^{\prime }\left(b\right)\cdot x}$

Strebt nun x gegen null, so streben offensichtlich sowohl a als auch b ebenfalls gegen null. Da $u^{\prime }\left(x\right)=2xund{v}^{\prime }\left(x\right)=\cos x$ ist, ergibt sich $\underset{a\to 0}{\lim }{u}^{\prime }\left(a\right)=0bzw.\underset{b\to 0}{\lim }{v}^{\prime }\left(b\right)=1$.

Demzufolge ist:
$\underset{x\to 0}{\lim }\frac{u^{\prime }\left(a\right)}{v^{\prime }\left(b\right)}=\frac{\underset{a\to 0}{\lim }{u}^{\prime }\left(a\right)}{\underset{b\to 0}{\lim }{v}^{\prime }\left(b\right)}=\frac{0}{1}=0$

Für $x<0$ sind die Überlegungen analog, so dass in der Tat gilt:
$\underset{x\to 0}{\lim }\frac{x^2}{\sin x}=0$

Dieses Ergebnis lässt sich zur (ersten) Regel von L'HOSPITAL verallgemeinern:

• Es seien die Funktionen $u\left(x\right)undv\left(x\right)$ in einer Umgebung von $x_0$ differenzierbar und ihre Ableitungsfunktionen in $x_0$ stetig.
  Ist nun $u\left(x_0\right)=v\left(x_0\right)=0$ sowie $v^{\prime }\left(x\right)\ne 0$ in einer Umgebung von $x_0$, so gilt:
  $\underset{x\to x_0}{\lim }\frac{u\left(x\right)}{v\left(x\right)}=\underset{x\to x_0}{\lim }\frac{u^{\prime }\left(x\right)}{v^{\prime }\left(x\right)}(falls\underset{x\to x_0}{\lim }\frac{u^{\prime }\left(x\right)}{v^{\prime }\left(x\right)}existiert)$

Anmerkungen: Die Regel von L'HOSPITAL kann (wenn jeweils die Voraussetzungen erfüllt sind) auch mehrfach hintereinander angewendet werden.
Zu beachten ist ferner, dass man Zähler- und Nennerfunktionen getrennt ableitet und nicht nach der Quotientenregel verfährt.

Beispiel 1: $\underset{x\to 1}{\lim }\frac{x^3-2x+1}{x^9-x^2}$

Es ist:
$\underset{x\to 1}{\lim }\frac{x^3-2x+1}{x^9-x^2}=\underset{x\to 1}{\lim }\frac{3x^2-2}{9x^8-2x}=\frac{3\cdot 1^2-2}{9\cdot 1^8-2\cdot 1}=\frac{1}{7}$

Beispiel 2: $\underset{x\to \frac{\pi }{2}}{\lim }\frac{\cos x}{\pi -2x}$

Für $x\to \frac{\pi }{2}$ gehen sowohl die Zählerfunktion $u\left(x\right)=\cos x$ als auch die Nennerfunktion $v\left(x\right)=\pi -2x$ gegen null, aber es ist nicht absehbar, was mit dem Quotienten passiert, deshalb überprüfen wir den Grenzwert des Quotienten der Ableitungen:
$\underset{x\to \frac{\pi }{2}}{\lim }\frac{u\left(x\right)}{v\left(x\right)}=\underset{x\to \frac{\pi }{2}}{\lim }\frac{u^{\prime }\left(x\right)}{v^{\prime }\left(x\right)}=\underset{x\to \frac{\pi }{2}}{\lim }\left(\frac{-\sin x}{-2}\right)=\underset{x\to \frac{\pi }{2}}{\lim }\frac{\sin x}{2}=\frac{1}{2}$
Also ist $\underset{x\to \frac{\pi }{2}}{\lim }\frac{\cos x}{\pi -2x}=\frac{1}{2}$.

Beispiel 3: $\underset{x\to 0}{\lim }\frac{e^x-x-1}{x^2}$

Für $x\to 0$ streben sowohl die Zähler- als auch die Nennerfunktion gegen null. Der Quotient der Ableitungen ist:
$\frac{u^{\prime }\left(x\right)}{v^{\prime }\left(x\right)}=\frac{e^x-1}{2x}$

Da wiederum Zähler- und Nennerfunktion für $x\to 0$ gegen null streben, wird ein weiteres Mal abgeleitet:
$\frac{u^{″}\left(x\right)}{v^{″}\left(x\right)}=\frac{e^x}{2}$

Jetzt ist $\underset{x\to 0}{\lim }\frac{e^x}{2}=\frac{1}{2}$ und demzufolge gilt:
$\underset{x\to 0}{\lim }\frac{e^x-x-1}{x^2}=\underset{x\to 0}{\lim }\frac{e^x-1}{2x}=\underset{x\to 0}{\lim }\frac{e^x}{2}=\frac{1}{2}$.

Anmerkung: Die Regel von L'HOSPITAL lässt sich nicht anwenden, wenn die Zähler- oder die Nennerfunktion einen endlichen von null verschiedenen Grenzwert hat. Zum Beispiel ist $\underset{x\to 0}{\lim }\frac{x}{x+\cos x}=\frac{0}{1}=0$. Eine formale (nicht die Voraussetzungen prüfende) Anwendung der Regel von L'HOSPITAL führt zu dem falschen Ergebnis $\underset{x\to 0}{\lim }\frac{x}{x+\cos x}=\underset{x\to 0}{\lim }\frac{1}{1-\sin x}=\frac{1}{1}=1$.

Greifen wir nochmals das Eingangsbeispiel auf.
Mithilfe der Regel von L'HOSPITAL erhält man:
$\underset{\begin{array}{l}R\to 0\\ R>0\end{array}}{\lim }\frac{U\cdot {\left(1-e\right)}^{-}{}^{\frac{R}{L}\cdot t}}{R}=\underset{\begin{array}{l}R\to 0\\ R>0\end{array}}{\lim }\frac{\frac{U}{L}\cdot t\cdot e^{-\frac{R}{L}\cdot t}}{1}=\frac{U}{L}\cdot t$

Im Unterschied zu den physikalischen Überlegungen erweckt das mathematische Resultat eine unbegrenzte Zunahme der Stromstärke mit der Zeit. Praktisch stellt sich jedoch ziemlich schnell der konstante Wert $\frac{U}{L}$ ein (s. obiges Textbild).