Taylor-Entwicklung einiger trigonometrischer Funktionen
Ist f eine nichtrationale Funktion mit der Gleichung y = f(x), dann ist es nicht möglich, zur Annäherung von y = f(x) ein Polynom n-ter Ordnung zu verwenden, dessen Koeffizienten mit den Ableitungen von y = f(x) an der Stelle in derselben Weise gebildet werden, wie die Koeffizienten der TAYLOR-Entwicklung einer ganzrationalen Funktion.
Dies ergibt sich bereits daraus, dass – im Unterschied zu ganzrationalen Funktionen n-ten Grades – die (n + 1)-te Ableitung und alle weiteren Ableitungen einer nichtrationalen Funktion im Allgemeinen nicht identisch gleich null sind.
Das heißt: Die Entwicklung einer solchen Funktion an einer Stelle „bricht nicht ab“, sondern würde zu einer Summe mit unendlich vielen Summanden (Reihe) führen. Man spricht deshalb auch von der Entwicklung einer Funktion in eine TAYLOR-Reihe.
An zwei Beispielen wird gezeigt, dass sich die Sinus- und auch die Kosinusfunktion in eine TAYLOR-Reihe entwickeln lassen.
TAYLOR-Entwicklung der Funktion f(x) = sin x
Die Sinusfunktion soll an der Stelle nach TAYLOR entwickelt werden.
Für die Funktion f und ihre Ableitungen gilt:
und damit allgemein (wie man durch vollständige Induktion zeigen kann) für
Im TAYLOR-Polynom der Sinusfunktion an der Stelle treten also nur Potenzen von x mit ungeraden Exponenten auf.
Mithilfe der allgemeinen taylorschen Formel erhalten wir
mit
Um beurteilen zu können, wie gut das in der obigen Gleichung aufgestellte TAYLOR-Polynom die Funktion f(x) = sin x an der Stelle approximiert, müssen wir das Restglied abschätzen:
Da konvergiert auch das Restglied gegen null.
Erst jetzt können wir davon sprechen, dass sich die Sinusfunktion in der Umgebung von 0 durch das TAYLOR-Polynom approximieren lässt bzw. dass die Sinusfunktion in eine TAYLOR-Reihe entwickelt wurde:
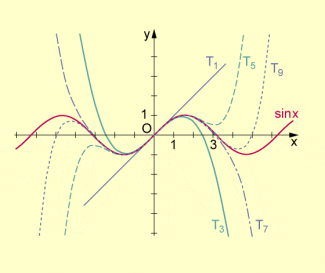
Die Abbildung zeigt die Sinusfunktion und die ersten fünf Schmiegparabeln.
(Man beachte, dass die Sinusfunktion eine ungerade Funktion ist.)
-
Sinusfunktion mit Schmiegparabeln
TAYLOR-Entwicklung der Funktion f(x) = cos x
Die Entwicklung der Kosinusfunktion erhält man auf analogem Wege:
Für die Ableitungen von f(x) = cos x gilt:
Daraus folgt für die Entwicklung an der Stelle
Bei festem x ist
Auch die Kosinusfunktion lässt sich also in eine TAYLOR-Reihe entwickeln. Demzufolge kann man die Werte von cos x für beliebige x mit jeder geforderten Genauigkeit berechnen.
Derartige Approximationen nichtrationaler Funktionen sind eine wichtige Grundlage für entsprechende Rechenprozesse in Taschenrechnern und Computern.

