Korrelation und lineare Regression

Wir betrachten die grafische Darstellung von Wertepaaren $(x_i;y_i)$ zweier Größen X und Y. Die Abhängigkeit dieser Größen voneinander nennt man Korrelation. Ein Maß für die Korrelation ist der sogenannte Korrelationskoeffizient:
$r_{xy}=\frac{{\displaystyle \sum _{i=0}^{k-1}(x_i-\overline{x})(y_i-\overline{y})}}{\sqrt{{\displaystyle \sum _{i=0}^k{(x_i-\overline{x})}^2}\cdot {\displaystyle \sum _{i=0}^k{(y_i-\overline{y})}^2}}}(\overline{x},\overline{y}\sin dMittelwertevon{x}_{i}bzw{y}_i.)$

Ist $–1\le r_{xy}\le \mathrm{1,}$ so heißen die Zufallsgrößen unkorreliert, wird ein hoher Korrelationskoeffizient ermittelt, kann ein kausaler Zusammenhang zwischen den Zufallsgrößen angenommen werden.

Die Ermittlung eines funktionalen Zusammenhangs zwischen X und Y führt zu einer Funktion, deren Graph möglichst nahe an allen Punkten liegt. Eine solche Funktion nennt man Regressionsfunktion, das Verfahren zu ihrer Ermittlung Regression.

Ist die Regressionsfunktion eine lineare Funktion, liegt eine lineare Regression vor, der dazugehörige Graph heißt dann Regressionsgerade.

Für eine lineare Regressionsfunktion $y=f(x)=mx+n$ gilt:
$\begin{array}{l}m=\frac{k\cdot {\displaystyle \sum _{i=0}^{k-1}{x}_i\cdot y_i-{\displaystyle \sum _{i=0}^{k-1}{x}_i\cdot }{\displaystyle \sum _{i=0}^{k-1}{y}_i}}}{k\cdot {\displaystyle \sum _{i=0}^{k-1}{x}_i{}^2-{({\displaystyle \sum _{i=0}^{k-1}{x}_i})}^2}}\\ n=\frac{{\displaystyle \sum _{i=0}^{k-1}{x}_i{}^2\cdot {\displaystyle \sum _{i=0}^{k-1}{y}_i}-{\displaystyle \sum _{i=0}^{k-1}{x}_i\cdot {\displaystyle \sum _{i=0}^{k-1}{x}_i\cdot }{y}_i}}}{k\cdot {\displaystyle \sum _{i=0}^{k-1}{x}_i{}^2-{({\displaystyle \sum _{i=0}^{k-1}{x}_i})}^2}}\end{array}$

Damit besteht die Möglichkeit, die Regressionsfunktion auch ohne vorherige Berechnung des Korrelationskoeffizienten zu bestimmen.

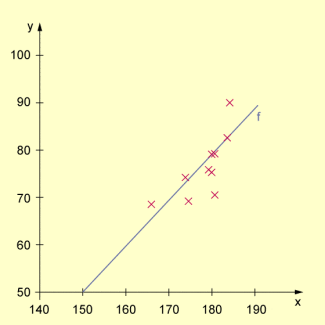
Beispiel: In einem Sportverein werden Körpergröße (Zufallsgröße X) und Körpergewicht (Zufallsgröße Y) von jugendlichen Sportlern (gleichen Geschlechts) gemessen. Dabei ergeben sich die folgenden Messwerte:

In der Annahme, dass zwischen Größe und Gewicht ein linearer Zusammenhang besteht, soll die Regressionsfunktion ermittelt und dargestellt werden.