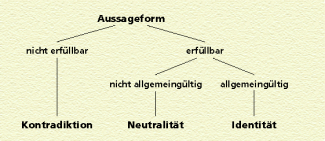
Aussageformen, Erfüllbarkeit

Eine Aussageform ist eine sinnvolle sprachliche Äußerung, die mindestens eine (freie) Variable enthält und die zur Aussage wird, wenn für die Variable(n) ein Element aus dem Grundbereich eingesetzt wird.

Dabei treten folgende Fälle auf:

• Kein Element des Grundbereichs überführt die Aussageform in eine wahre Aussage, d. h., die Aussageform ist nicht erfüllbar (unerfüllbar).
• Wenigstens ein Element des Grundbereichs überführt die Aussageform in eine wahre Aussage. Man sagt, die Aussageform ist erfüllbar.
• Alle Elemente des Grundbereichs überführen die Aussageform in eine wahre Aussage. Die Aussageform ist dann allgemeingültig.

Mit erfüllbaren Aussageformen können wahre Existenzaussagen gebildet werden.

Beispiel:
Ein Viereck ist ein Quadrat. (Aussageform, keine Aussage!)
Es gibt ein Viereck, das ein Quadrat ist. (wahre Aussage)
Aber: Nicht jedes Viereck ist ein Quadrat.

Mit allgemeingültigen Aussageformen können wahre Allaussagen gebildet werden.

Beispiel:
$a\cdot b=b\cdot a\left(a,b\in ℝ\right)$ (allgemeingültige Aussageform)
Für alle reelllen Zahlen gilt: Faktoren kann man vertauschen, das Produkt bleibt dabei gleich. (wahre Allaussage)