Daten, Auswerten

Für häufig wiederkehrende Berechnungen enthalten Tabellenkalkulationsprogramme vorbereitete Formeln (sogenannte Funktionen), die an den entsprechenden Stellen nur noch einzufügen und durch spezielle Eingaben zu ergänzen sind.

Ein typisches Beispiel ist die Funktion WURZEL, mit deren Hilfe Näherungswerte beliebiger Quadratwurzeln ermittelt werden. Aber auch viele Rechnungen zur Auswertung von Daten können mithilfe solcher Funktionen effektiv und schnell ausgeführt werden.

Man findet die Funktionen im Menü Einfügen/Funktion oder mithilfe der Schaltfläche „Funktions-Assistent“. Sind von der Funktion Name und Schreibweise (ihre „Syntax“) bekannt, kann sie auch direkt in die betreffende Zelle eingetragen werden. Dabei ist wieder mit dem Gleichheitszeichen zu beginnen.

Beispiel:
In einer Sportgruppe wurden von 15 Jungen folgende Körpergrößen gemessen (Angabe in Zentimeter): 171, 175, 178, 178, 176, 177, 182, 175, 178, 180, 178, 177, 182, 170

Zur Beschreibung dieser Stichprobe sollen wesentliche Lage- und Streumaße bestimmt werden. Zentralwert z (Median) und Modalwert m können nach vorherigem Ordnen sofort abgelesen werden; es sind z = 1777 und m = 178.
Das Ordnen der vorher in beliebiger Reihenfolge eingegebenen Messwerte erfolgt über die Sortierfunktion im Menü Daten.

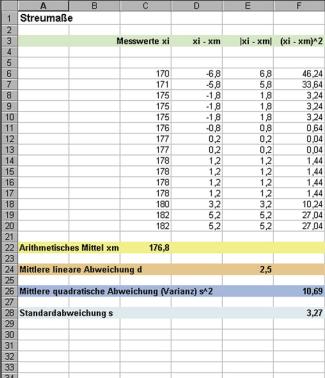
Das arithmetische Mittel x_m und die Streumaße sollen mithilfe einer Kalkulationstabelle ermittelt werden. In Spalte C werden die Messwerte x_iund in Zelle C22 die Formel zur Berechnung von x_m eingetragen (=MITTELWERT(C6:C20)).
Als Näherungswert erhält man sofort x_m= 176,8.

Die mittlere lineare Abweichung

d = $\frac{{\text{|x}}_{\text{1}}{\text{ – x}}_{\text{m}}{\text{| + |x}}_{\text{2}}{\text{ – x}}_{\text{m}}\text{| + }\mathrm{...}{\text{ + |x}}_{\text{n}}{\text{ – x}}_{\text{m}}\text{|}}{\text{n}}$ wird mithilfe der Spalte D und E berechnet. Dazu wird in Zelle D6 die Zellenverknüpfung = C6 – C$22 eingetragen und durch Ziehen auf die Zelle D7 bis D20 kopiert. Da die Summe der Abweichungen x_i – x_mstets gleich 0 ist, muss beim Berechnen der mittleren Abweichung mit den Beträgen der einzelnen Abweichungen vom arithmetischen Mittel gearbeitet werden. Deshalb werden in Spalte E die entsprechenden Absolutwerte gebildet (=ABS(D6) in Zelle E6 und nachfolgendes Kopieren). Über =MITTELWERT(E6:E20) erhält man schließlich in E24 einen Näherungswert für die mittlere lineare Abweichung.

Um das (zumindest ohne entsprechende Hilfsmittel) nicht immer einfache Rechnen mit Beträgen zu vermeiden, verwendet man in der Praxis häufig zwei andere Streumaße, die mittlere quadratische Abweichung (Varianz) s² und die Standardabweichung s.
Es gilt: s² = $\frac{{\left({\text{x}}_{\text{1}}{\text{ – x}}_{\text{m}}\right)}^2+{\left({\text{x}}_{\text{2}}{\text{ – x}}_{\text{m}}\right)}^2+\mathrm{...}+{\left({\text{x}}_{\text{n}}{\text{ – x}}_{\text{m}}\right)}^2}{\text{n}}$
s = $\sqrt{\frac{{\left({\text{x}}_{\text{1}}{\text{ – x}}_{\text{m}}\right)}^2+{\left({\text{x}}_{\text{2}}{\text{ – x}}_{\text{m}}\right)}^2+\mathrm{...}+{\left({\text{x}}_{\text{n}}{\text{ – x}}_{\text{m}}\right)}^2}{\text{n}}}$

Spalte F liefert die Quadrate der linearen Abweichung (=D6^2 in Zelle F6 eintragen und durch Ziehen auf F7 bie F20 kopieren) und Zelle F26 (=MITTELWERT (F6:F20)) die mittlere quadratische Abweichung. Mit =WURZEL(F26) liefert Zelle F28 letztlich einen Näherungswert für die Standardabweichung.

Auch wenn das Einrichten des hier verwendeten Rechenblatts recht aufwendig erscheint, sind die Berechnungen doch erheblich einfacher als mit einem Taschenrechner. Besonders vorteilhaft erweist sich, dass die Rechenblätter sofort für andere Eingangswerte verwendet werden können.

Oft ist es sinnvoll, die vorhandenen Daten in Klassen zusammenzufassen. Im Beispiel oben erfolgt die Klassenbildung durch Vorgabe der Intervallgrenzen 170 cm, 175 cm und 180 cm in Spalte B. Die Häufigkeitsverteilung kann mithilfe der Funktion HÄUFIGKEIT erzeugt werden. Da mit drei vorgegebenen Intervallgrenzen vier Intervalle festgelegt werden (0 bis 170, 171 bis 175, 176 bis 180, über 180), müssen vor Anwendung des Befehls vier Zellen einer Spalte (hier C) markiert werden. Wichtig ist, dass die Eingabe des Befehls nicht mit OK oder ENDE, sondern mit STRG + UMSCHALT + EINGABE abgeschlossen wird. Detaillierte Hinweise sind unter dem Suchbegriff „Häufigkeit“ im Programm zu finden.
Die Häufigkeitsverteilung kann dann als Streifendiagramm dargestellt werden.