Diophantische Gleichungen

Lineare Gleichungen mit zwei gesuchten (freien) Variablen haben im Bereich der reellen Zahlen $ℝ$ unendliche viele Lösungen. Dies sind Zahlenpaare, die diese Gleichungen erfüllen.
Für a, b, c, x, y $\in$ $ℝ$ gibt es unendliche viele Paare (x; y), für die die Gleichung ax +by + c = 0 zu einer wahren Aussage wird.

Anders sieht es aus, wenn der Variablengrundbereich für x und y eingeschränkt wird.

Beispiel:
Die Gleichung 5x +3y + 2 = 0 hat weder im Bereich der natürlichen Zahlen $\mathbb{N}$ noch im Bereich der gebrochenen Zahlen $\mathbb{Q}$+ eine Lösung.

Wird in der linearen Gleichung ax + by = c der Variablengrundbereich für a, b, c, x und y auf die Menge der ganzen Zahlen eingeschränkt, so spricht man von diophantischen Gleichungen.

Diese Form der Gleichungen wurde nach dem griechischen Mathematiker DIOPHNTOS VON ALEXANDRIA (um 250), der sich ausführlich mit dem Lösen derartiger Gleichungen beschäftigte, benannt (wobei er allerdings für x und y auch Werte aus $ℝ$ zuließ).

Analog kann man auch diophantische Ungleichungen oder diophantische Gleichungen mit mehr als zwei Variablen oder von höherem Grad definieren.

Zum Lösen diophantischer Gleichungen lassen sich Zahlenkongruenzen nutzen. Das Vorgehen wird im Folgenden an einem Beispiel dargestellt.

Beispiel:
Zu lösen ist die diophantische Gleichung 3x + 2y = 5.

Von 3x + 2y = 5 wird übergegangen zu 3x + 2y $\equiv$5 (mod 3). Damit man erhält 2y $\equiv$2 (mod 3), woraus als einzige Lösung folgt:
y $\equiv$1 (mod 3)

Das heißt: Zur Lösungsmenge der Gleichung 3x + 2y = 5 gehören alle y, mit y = 3g + 1 (g $\in$ $\mathbb{Z}$).

Aus 3x + 5y = 5 erhält man dann:
3x + 2(3g + 1) = 5
3x + 6g + 2 = 5
3x + 6g = 3
x = 1 – 2g

Die Lösungsmenge ist also die Menge aller Zahlenpaare (x; y) mit
x = 1 – 2g und y = 3g + 1, d. h.:
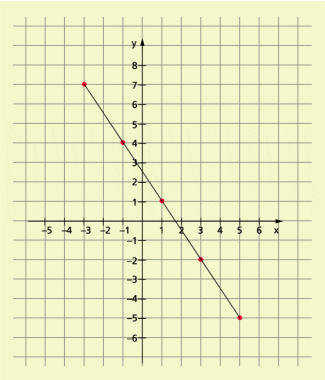
L = {...(5; –5), (3; –2), (1; 1), (–1; 4), (–3; 7), ...}

Man kann die Lösungen der Gleichung 3x + 2y = 5 grafisch darstellen, indem man zur Funktionsgleichung $y=-\frac{3}{2}x+\frac{5}{2}$ übergeht und deren Bild zeichnet. Die Lösungen sind dann alle Punkte des Graphen mit ganzzahligen Koordinaten (Bild 2).

Die Lösungsmenge dieser diophantischen Gleichung ist unendlich.

Für diophantische Gleichungen gilt:

Die Lösungsmenge einer diophantischen Gleichung
ax + by = c
ist entweder unendlich oder leer, d. h., es gibt entweder unendlich viele Lösungen oder keine Lösung.

Die Lösungsmenge ist genau dann nicht leer, wenn der größte gemeinsame Teiler von a und b ein Teiler von c ist.
Wenn a und b teilerfremd sind, ist ihr größter gemeinsamer Teiler gleich 1 und damit natürlich Teiler von c, es gibt in diesem Fall also unendlich viele Lösungen.

Wenn bei diophantischen Gleichungen der Variablengrundbereich weiter eingeschränkt wird (z. B. auf die Menge der natürlichen Zahlen) oder andere einschränkende Bedingungen gesetzt werden, kann die Lösungsmenge endlich sein.

Dies ist oftmals bei entsprechenden Anwendungsaufgaben der Fall.

Beispiel:
Der Betrag von 34$€$ soll aus Münzen zu 2$€$ und Scheinen zu 5$€$ zusammengesetzt werden. Welche Möglichkeiten gibt es?
Lösungsweg:
Es sei x die Anzahl der 2-Euro-Münzen und y die Anzahl der 5-Euro-Scheine.
   Dann gilt:
   2x + 5 y = 34 (ggT(2; 5) = 1, also existieren Lösungen)
   2x + 5 y $\equiv$ 34 (mod 5)
   2x $\equiv$ 34 (mod 5)
   2x $\equiv$ 4 (mod 5)
     x $\equiv$ 2 (mod 5)
Also gilt für x = 2; 7; 12; 17 und für y = 6; 4; 2; 0.

Ergebnis: Nur die drei Zahlenpaare (2; 6), (7; 4) und (12; 2) erfüllen die Bedingungen der Aufgabe, die Lösungsmenge ist also endlich.