Einsetzungsverfahren

Wenn eine der beiden linearen Gleichungen in die andere Gleichung des linearen Gleichungssystems „eingesetzt“ wird, um die Lösung des Gleichungssystems zu bestimmen, so nennt man dieses Verfahren Einsetzungsverfahren.

Ein lineares Gleichungssystem mit zwei Variablen wird mit dem Einsetzungsverfahren in folgenden Schritten gelöst:

1. Es wird – falls nötig – eine der beiden linearen Gleichungen nach einer der beiden Variablen umgeformt.
2. Die umgeformte Gleichung wird für die Variable in die andere Gleichung eingesetzt.
3. Die so entstandene lineare Gleichung mit nur einer Variablen wird gelöst.
4. Die erhaltene Lösung wird in eine der beiden Ausgangsgleichungen I oder II eingesetzt und die Gleichung gelöst.
5. Man führt eine Probe mit beiden Ausgangsgleichungen durch.
6. Die Lösungsmenge des Gleichungssystems wird angegeben.

$\begin{array}{l}\text{Probe:}\\ \text{Gleichung I}\text{Gleichung}\text{II}\\ \text{li}\text{. S}\text{. }\text{5}\cdot \left(-\text{3}\right)-\text{2}\cdot \text{4}=-\text{15}-\text{8}=-\text{23}-\text{6}\cdot \left(-\text{3}\right)+\text{3}\cdot \text{4}=\text{18}+\text{12}=\text{30}\\ \text{re}\text{. S}\text{.}-\text{23}\text{30}\\ \text{Vergleich }-\text{23}=-\text{23}\text{30}=\text{30}\\ \text{Lösungsmenge:}\text{L}=\left\{\left(-\text{3;}\text{4}\right)\right\}\end{array}$

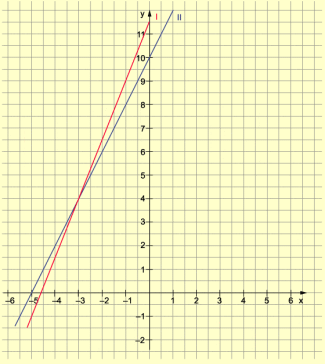
Die Lösung des linearen G leichungssystems lässt sich auch grafisch veranschaulichen.