Gleichsetzungsverfahren

Werden die beiden linearen Gleichungen des linearen Gleichungssystems nach derselben Variablen aufgelöst und die entsprechenden Terme gleichgesetzt, um die Lösung des Gleichungssystems zu bestimmen, so nennt man dieses Verfahren Gleichsetzungsverfahren.

Ein lineares Gleichungssystem mit zwei Variablen wird mit dem Gleichsetzungsverfahren in folgenden Schritten gelöst:

1. Es werden – falls nötig – beide lineare Gleichungen nach derselben Variablen aufgelöst.
2. Die erhaltenen Terme werden gleichgesetzt.
3. Die so entstandene lineare Gleichung mit nur einer Variablen wird gelöst.
4. Die erhaltene Lösung wird in eine der beiden Ausgangsgleichungen I oder II eingesetzt und die Gleichung gelöst.
5. Mit beiden Gleichungen wird die Probe ausgeführt.
6. Die Lösungsmenge der linearen Gleichungssystems wird angegeben.

Beispiel:

$\begin{array}{l}\text{I}\text{y}=\text{x}+\text{2}\\ \text{II}\text{y}+\text{3}\text{x}=\text{6}\\ \text{II}\text{a}\text{y}=-\text{3}\text{x}+\text{6}\\ \text{I}\text{und}\text{II}\text{a}\text{gleichsetzen}\\ \text{x}+\text{2}=-\text{3}\text{x}+\text{6}|-\text{2}\\ \text{x}=-\text{3}\text{x}+\text{4}|\text{+}\text{3}\text{x}\\ \text{4}\text{x}=\text{4}|\text{:}\text{4}\\ \text{x}=\text{1}\\ \text{in I}x=1einsetzen\\ y=1+2\\ y=3\\ \text{Probe:}\\ \text{Gleichung I }\text{Gleichung II}\\ \text{linke S}\text{. }\text{3}3+3\cdot 1=3+3=6\\ \text{rechte S}\text{. }1+2=3\text{6}\\ \text{Vergleich }3=36=6\\ \text{Lösungsmenge }L=\left\{\left(1;3\right)\right\}\end{array}$

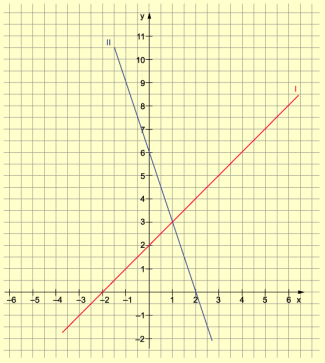
Die Lösung des linearen Gleichungssystems lässt sich auch grafisch veranschaulichen.

Anzahl der Lösungen von linearen Gleichungssystemen
Ein lineares Gleichungssystem hat genau eine Lösung, keine Lösung oder unendlich viele Lösungen.

• 1. Fall: Gleichungssystem hat genau eine Lösung
  Wenn das lineare Gleichungssystem genau eine Lösung hat, dann kann genau ein Wert für die Variable x und genau ein Wert für die Variable y bestimmt werden, d. h., die Lösungsmenge besteht aus genau einem Zahlenpaar (x; y): $\text{L}=\left\{\left(\text{x;}\text{y}\right)\right\}$
   
• 2. Fall: Gleichungssystem hat keine Lösung
  Wenn das lineare Gleichungssystem keine Lösung hat, dann gibt es keine Einsetzungen für die Variable x und keine Einsetzungen für die Variable y, d. h., es gibt kein Zahlenpaar, welches beide Gleichungen gleichzeitig erfüllt; also ist die Lösungsmenge leer:
  $\text{L}=\left\{\right\}$
  Egal welchen Wert man für die Variablen x und y beim rechnerischen Lösen einsetzt, es muss immer eine falsche Aussage entstehen, d. h. aber auch, dass die Variablen x und y keinen Einfluss mehr auf die linearen Gleichungen haben, weil sie nicht mehr darin vorkommen.
  
  Beispiel:
  $\begin{array}{l}\text{I}\text{3}\text{x}+\text{5}\text{y}=\text{18}\\ \text{II}-\text{3}\text{x}-\text{5}\text{y}=\text{20}\\ \text{I}+\text{II}\text{0}=\text{38}\text{falsche}\text{Aussage}\\ \text{Lösungsmenge:}\text{L}=\left\{\right\}\end{array}$
   
• 3. Fall: Gleichungssystem hat unendlich viele Lösungen
  Wenn das lineare Gleichungssystem in Abhängigkeit vom Grundbereich unendlich viele Lösungen hat, dann muss es unendlich viele Zahlenpaare geben, die beide Gleichungen gleichzeitig erfüllen. Dazu müssen beide Gleichungen identisch sein oder beim rechnerischen Lösen muss immer eine wahre Aussage entstehen, egal welchen Wert wir für die Variablen x und y einsetzen.
  
  Beispiel:
  $\begin{array}{l}\text{I}\text{2}\text{x}+\text{6}\text{y}=\text{20}\\ \text{II}\text{x}=-\text{3}\text{y}+\text{10}\\ \text{In}\text{I}-\text{3}\text{y}+\text{10}\text{für}\text{x}\text{einsetzen}\\ \text{2}\cdot \left(-\text{3}\text{y}+\text{10}\right)+\text{6}\text{y}=\text{20}\\ -\text{6}\text{y}+\text{20}+\text{6}\text{y}=\text{20}\\ \text{20}=\text{20}\text{wahre Aussage}\end{array}$
  Einige Lösungen des linearen Gleichungssystems sind:
  $\text{L}=\left\{\left(\text{4;}\text{2}\right)\text{,}\left(\text{7;}\text{1}\right)\text{,}\left(\text{10;}\text{0}\right)\text{,}\left(\text{13;}-\text{1}\right)\text{,}\mathrm{...}\right\}$
  Eine vollständige Angabe aller Zahlenpaare ist aber nicht möglich.