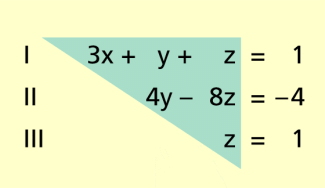Gleichungssysteme, drei Gleichungen
Jede Lösung eines Gleichungssystems aus drei Gleichungen mit drei Variablen ist ein Zahlentripel. Beim Lösen von linearen Gleichungssystemen mit mehr als zwei Gleichungen und Variablen geht man systematisch vor.
Gleichungen der Form ax + by + cz = d mit den Variablen x, y, z (a, b, c, d ) heißen lineare Gleichungen mit drei Variablen. Jede Lösung einer solchen Gleichung ist ein Zahlentripel.
Beim Lösen von linearen Gleichungssystemen mit mehr als zwei Gleichungen und Variablen geht man systematisch vor. Es kann in Verallgemeinerung des Einsetzungsverfahrens auf folgende Weise gelöst werden:
(1) Eine Gleichung wird nach einer Variablen aufgelöst und in allen anderen Gleichungen wird die Variable durch den erhaltenen Term ersetzt.
(2) Der Schritt (1) wird so lange fortgesetzt, bis nur noch eine Gleichung vorhanden ist. Dann können für alle anderen Variablen wieder schrittweise Werte oder Terme ermittelt werden.
In vielen Fällen lässt sich jedoch durch geschicktes Addieren oder Subtrahieren zweier Gleichungen eine günstige Umformung des Systems erreichen, die schneller zum Ziel führt.
Hat der linke Teil eines Systems die Form eines Dreiecks (Beispiel im Bild unten), kann man durch „Rückwärtseinsetzen“ das System lösen:
| I | x + y + z = 1 | ||
| II | 4y – 8z = –4 | mit a = 0 | |
| III | z = 1 | mit a = 0, b = 0 |
Ziel ist es, das System so umzuformen, dass eine Dreiecksform entsteht. Dazu kann das Additionsverfahren benutzt werden. Äquivalente Umformungen sind u. a.:
- Gleichungen vertauschen
- Beide Seiten einer Gleichung mit derselben von 0 verschiedenen Zahl multiplizieren
- Beide Seiten einer Gleichung durch dieselbe von 0 verschiedene Zahl dividieren
- Eine Gleichung zu einer anderen Gleichung addieren
- Eine Gleichung von einer anderen Gleichung subtrahieren
| Aus III ergibt sich sofort: | z = 1 | |
| z = 1 in II einsetzen und nach y auflösen: | 4y - 8 · 1 = -4 y = 1 | |
| z = 1 und y = 1 in I einsetzen und nach x auflösen: | x + 1 + 1 = 1 x = -1 |
Probe durch einsetzen der Werte für x, y und z in das ursprüngliche lineare Gleichungssystem:
| linke Seite | rechte Seite | Vergleich |
| I -1 + 1 + 1 = 1 | 1 | 1 = 1 w. A. |
| II 4 · 1 – 8 · 1 = -4 | -4 | -4 = -4 w. A. |
| III 1 = 1 | 1 | 1 = 1 w. A. |
Die Lösungsmenge ist L = {(1|1|-1)}.
Diese Vorgehensweise zum Lösen von Gleichungssystemen heißt gaußscher Algorithmus.
-
Gleichungssystem in Dreiecksform