Goldener Schnitt
Zum Begriff und zur Geschichte
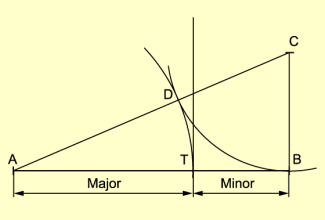
Der Goldene Schnitt teilt eine Strecke so, dass das Ganze AB zum größeren Teil (Major, lat. das Größere) AT = M im gleichen Verhältnis steht wie der größere zum kleineren Teil (Minor, lat. das Kleinere) BT = m (Bild 1).
Es gilt:
Die Strecke heißt stetig geteilt oder nach dem Goldenen Schnitt geteilt. Dieses Teilungsverhältnis kann man auch berechnen:
Es aber ist keine rationale Zahl, sondern die goldene Schnittzahl, eine irrationale Zahl (etwa 1,618).
Bei Einführung der Unbekannten x = AT und der Bezeichnung der Strecke AB = a entspricht demnach der Goldene Schnitt der Konstruktion der (positiven) Lösung der Gleichung
.
Es ergibt sich:
Die Bezeichnung stetige Teilung wurde Mitte des 19. Jh. gebräuchlich und geht auf folgende Eigenschaft dieser Teilung zurück: Trägt man den kürzeren auf den längeren Abschnitt ab, so wird dieser im gleichen Verhältnis geteilt wie die Ausgangsstrecke. Dies kann man nun beliebig fortsetzen, wobei das Teilungsverhältnis konstant, eben stetig, erhalten bleibt.
Goldener Schnitt
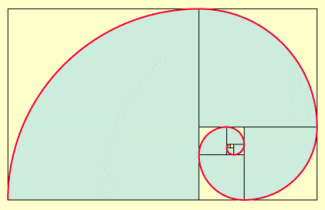
Dies kann man auch auf ein Rechteck übertragen, dessen Seiten Minor m bzw. Major M einer stetig geteilten Strecke a sind. Ein solches Rechteck nennt man auch goldenes Rechteck. Trennt man von diesem den quadratischen Teil m² ab, so erhält ein zum Ausgangsrechteck ähnliches Restrechteck mit den Seiten m und
M – m. Diese Abtrennung ist fortsetzbar und liefert eine Spirale von immer kleiner werdenden Quadraten, die sich um einen gewissen Ausgangspunkt herum windet. Mit Viertelkreisen in den Quadraten erhält man die sogenannte goldene Spirale (Bild 2).
Goldene Spirale
Ausgangspunkt für die Entdeckung dieses besonderen Teilungsverhältnisses war das regelmäßige Fünfeck oder besser der sich daraus ergebende regelmäßige fünfeckige Stern – das Pentagramm – das Geheimzeichen des Bundes der Pythagoreer, einer Wissenschaftsschule in der Antike, die von PYTHAGORAS VON SAMOS begründet wurde (Bild 3). Die Leitidee dieser Schule („Alles ist Zahl“) war es, die natürlichen Zahlen als „Urprinzip aller Dinge“ zu verstehen.
Jedes Wissen und jedes Ding sollte seinen Ursprung in den Zahlen haben oder sich durch sie erklären und beschreiben lassen. Mit dieser Ansicht glaubten sich die Pythagoreer dem normalen Volk überlegen. Nun war es aber gerade einer der ihren, der zeigte, dass es etwas gab, was sich nicht mit natürlichen Zahlen und Proportionen beschreiben ließ.
Pentagramm
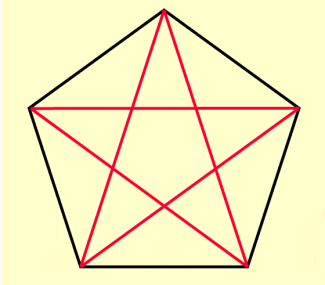
Der Pythagoreer HIPPASOS VON METAPONT (5. Jh. v. Chr.) entdeckte das Pentagon-Dodekaeder und fand bei der Untersuchungen des Verhältnisses von Seiten und Diagonalen eben des Pentagramms – des Geheimzeichen der Schule – , dass sich die Diagonalen stetig teilen und die Seitenlänge dem größeren Teilstück gleich ist (Bild 4). Er berechnete das Verhältnis von Diagonale zu Seite mit 1,681... und fand dafür keine Darstellung mit natürlichen Zahlen, wie es die pythagoreische Proportionenlehre vorgab. Er suchte umsonst, denn dies ist, wie wir heute wissen, keine rationale, sondern eine irrationale Zahl. Hieran zerbrach die Schule, da sie ihrer Leitidee beraubt war. HIPPASOS wurde vermutlich im Meer ertränkt.
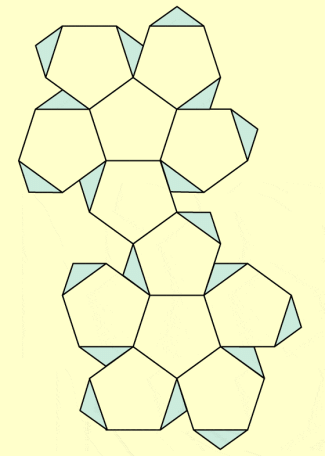
Netz eines Dodekaeders
Die Bezeichnung sectio aurea (Goldener Schnitt) stammt erst aus dem Mittelalter und lässt erkennen, dass dieser Proportion besondere Bedeutung beigemessen wurde. LUCA PACCIOLI (1445 bis 1514), Mönch und Mathematiker aus Florenz, benutzte zu Beginn des 16. Jh. vermutlich als erster den Namen divina proportio (göttliche Teilung), der auf seine Hochachtung gegenüber dem Goldenen Schnitt hindeutet.
JOHANNES KEPLER (1571 bis 1630), Mathematiker, Physiker und Astronom, bezeichnete sie ebenfalls als sectio divina (göttlicher Schnitt).
Im Mittelalter verwendete man das Pentagramm auch als Zauberzeichen gegen böse Geister („Drudenfuß“).
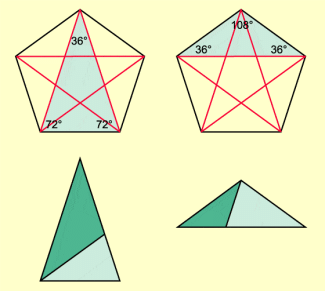
In diesem Sternfünfeck verstecken sich aber auch noch zwei aus mathematischer Sicht hervorzuhebende gleichschenklige Dreiecke und dies auch gleich mehrfach. Ein spitzwinkliges mit den Winkeln von 36° und zweimal 72° sowie ein stumpfwinkliges mit den Winkeln von 108° und zweimal 36°. Diese Dreiecke heißen ebenfalls goldene Dreiecke. Jedes dieser beiden Dreiecke lässt sich wiederum in zwei goldene Teildreiecke zerlegen (Bild 6).
Konstruktion der stetigen Teilung
Konstruktionsbeschreibung (Simulation):
- Zeichnen der Strecke AB
- C ist der Schnittpunkt der Senkrechten zu AB in B und des Kreises um B mit den Radius .
- D ist der Schnittpunkt von AC und des Kreises um C mit dem Radius .
- Der Teilungspunkt T ist der Schnittpunkt von AB und des Kreises um A mit dem Radius r = AD.
Pentagramm
goldenes Dreieck interaktiv goldenes Rechteck Goldener Schnitt Pentagramm göttlicher Schnitt Simulation goldene Spirale göttliche Teilung stetige Teilung Geonet Teilungsverhältnis
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 