Strahlensätze
Eine Figur aus zwei Strahlen mit gemeinsamem Anfangspunkt Z, die von zwei zueinander parallelen Geraden geschnitten wird, heißt Strahlensatzfigur mit dem Zentrum Z.
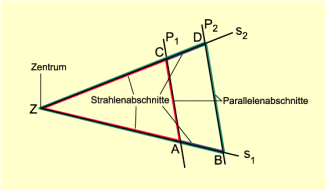
Eine Figur aus zwei Strahlen mit gemeinsamem Anfangspunkt Z (Strahlenbüschel), die von zwei zueinander parallelen Geraden geschnitten wird, heißt Strahlensatzfigur mit dem Zentrum Z (Bild 1).
Die Strecken ZA, ZB, ZC, ZD, AB und CD heißen Strahlenabschnitte. Die Strahlenabschnitte ZA und ZC, ZB und ZD sowie AB und CD heißen gleichliegend.
Die Strecken AC und BD heißen Parallelenabschnitte.
Dem Parallelenabschnitt AC sind die Strahlenabschnitte ZA und ZC zugeordnet.
-
Strahlensatzfigur
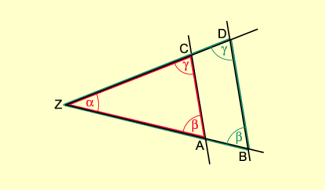
Eine Strahlensatzfigur enthält zwei Dreiecke, das Dreieck ZAC und das Dreieck ZBD (Bild 2). Die Dreiecke sind zueinander ähnlich, da die Innenwinkel gleich groß sind (Stufenwinkel).
-
Ähnliche Dreiecke
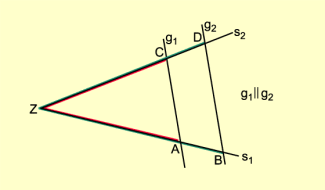
1. Strahlensatz:
In einer Strahlensatzfigur ist das Verhältnis zweier Strahlenabschnitte auf einem Strahl genauso groß wie das Verhältnis der gleichliegenden Strahlenabschnitte auf dem anderen Strahl (Bild 3):
2. Strahlensatz:
In einer Strahlensatzfigur ist das Verhältnis der Parallelenabschnitte genauso groß wie das Verhältnis der zugeordneten Strahlenabschnitte auf demselben Strahl:
-
Strahlensatzfigur
Besteht das Strahlenbüschel aus mehr als zwei Strahlen, lassen sich weitere Verhältnisgleichungen aufstellen. So verhalten sich die zwischen zwei Strahlen des Büschels gelegenen Parallelenabschnitte auf zwei Parallelen wie die zwischen zwei anderen Strahlen liegenden Abschnitte auf denselben Parallelen (Bild 4):
-
Strahlensatzfigur mit drei Strahlen
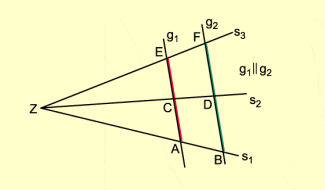
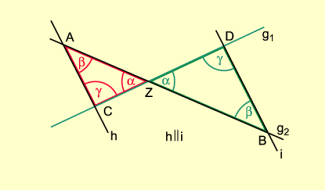
Die Strahlensätze gelten analog auch für eine Figur aus zwei oder mehreren einander schneidenden Geraden, die durch zwei zueinander parallele Geraden geschnitten werden. Die Dreiecke ZAC und ZBD in Bild 5 sind zueinander ähnlich, da sie in den Winkeln übereinstimmen (Scheitelwinkel und Wechselwinkel).
-
Strahlensatzfigur mit sich schneidenden Geraden