Gradmaß, Bogenmaß
Eine Möglichkeit, eine Maßeinheit zum Messen von Winkeln zu erhalten, ist die Teilung eines Kreises durch Radien in deckungsgleiche Teile (Kreissektoren). Dies führt zum Gradmaß.
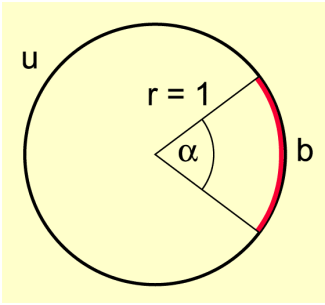
Wählt man den Radius 1 (also den Einheitskreis), kann zu jedem Winkel die Länge des Kreisbogens b angegeben werden.
Das Bogenmaß b eines Winkels ist die Maßzahl der Länge des zugehörigen Kreisbogens auf dem Einheitskreis.
Winkelmaße
Alle Winkelmaße beruhen auf Teilungen des Kreises.
Eine Möglichkeit, eine Maßeinheit zum Messen von Winkeln zu erhalten, ist die Teilung eines Kreises durch Radien in deckungsgleiche Teile (Kreisausschnitt, Kreissektor). Dies führt zum Gradmaß.
Grad (Altgrad)
Winkel der Größe 1 Grad erhält man, indem man einen Kreis durch Radien in 360 deckungsgleiche Kreissektoren zerlegt.
Jedes Teil hat die Größe 1º (1 Grad). Kleinere Einheiten sind 1' (1 Minute) und 1'' (1 Sekunde).
Es ist: 1º = 60'sowie 1' = 60''
Diese bis heute gebräuchliche Teilung des Kreises in 360 Teile hat ihre historischen Wurzeln bei den Sumerern, die ein Zahlensystem mit der Basis 60 hatten. Diese Einteilung hat gegenüber einer Teilung des Kreises in 100 oder 400 Teile wesentliche Vorteile. Nimmt man den Vollwinkel mit 360º an, kann die Größe vieler uns gebräuchlicher Winkel bequem ausgedrückt werden, weil 360 eine große Anzahl Teiler besitzt. Insbesondere sind auch Drittelungen usw. gut möglich.
Gon (Neugrad)
Winkel der Größe 1 Neugrad (1 Gon) erhält man, indem man einen Kreis durch Radien in 400 deckungsgleiche Kreisausschnitte zerlegt.
Jedes Teil hat die Größe (1 Gon). Kleinere Einheiten sind
( 1 Neuminute) und ( 1 Neusekunde).
Es ist: = sowie =
-
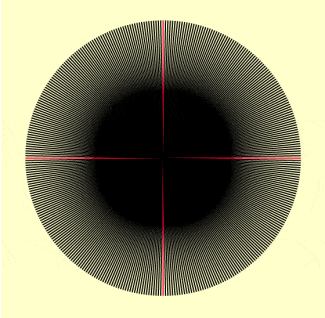
Teilung des Kreises in 360 kongruente Kreisausschnitte
Bogenmaß und Radiant
Das Bogenmaß als Einheit zum Messen von Winkeln ergibt sich so:
In jedem Kreissektor ist die Länge des Kreisbogens b proportional zum Zentriwinkel (Mittelpunktswinkel) des Kreissektors und zum Radius r des Kreises. Ist b die Länge des Bogens und die Größe des zugehörigen Zentriwinkels, so ist ausgehend vom Umfang des Kreises
bzw. umgeformt .
Wählt man den Radius 1 (also den Einheitskreis), kann zu jedem Winkel die Länge des Kreisbogens b angegeben werden. Das Bogenmaß b eines Winkels ist die Maßzahl der Länge des zugehörigen Kreisbogens auf dem Einheitskreis:
Die Einheit im Bogenmaß ist der Radiant (1 rad).
1 rad ist der Winkel, für den der Bogen auf dem Einheitskreis die Länge 1 hat. Es gilt:
1 rad = 57° 17´45´´
rad = 0,017453 rad
Bei der Angabe von Winkelgrößen im Bogenmaß wird auf die Einheit rad meist verzichtet:
-
Kreisbogen am Einheitskreis
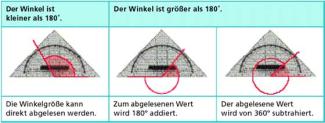
Winkelmessung mit dem Geodreieck zeigt das Bild 3.
Der Unterschied zwischen einem Winkel und seiner Größe wird hier nicht durch unterschiedliche Symbole ausgedrückt, weil aus dem Zusammenhang hervorgeht, ob ein Winkel oder seine Größe gemeint ist.
Die Schreibweise = 60º bedeutet, dass der Winkel eine Größe von 6 0 Grad hat.
-
Winkelmessung mit dem Geodreieck
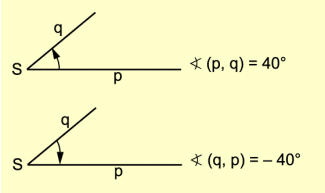
Größenangabe orientierter Winkel
Bei der Angabe der Größe orientierter Winkel ist es erforderlich, auch die Orientierung des Winkels zu nennen.
Die Winkel (p, q) und (q, p) sind betragsmäßig gleich, aber entgegengesetzt orientiert. Drehungen entgegen dem Uhrzeigersinn entspricht die positive Orientierung. Das entsprechende Winkelmaß hat ein positives Vorzeichen. Drehungen im Uhrzeigersinn entspricht die negative Orientierung. Das entsprechende Winkelmaß hat ein negatives Vorzeichen.
-
Größenangabe orientierter Winkel