Winkel an Geraden
Schneiden einander zwei Geraden, so heißen die gegenüberliegenden Winkel Scheitelwinkel und die nebeneinanderliegenden Winkel Nebenwinkel.
Schneiden zwei verschiedene parallele Geraden eine dritte Gerade, so entstehen acht Winkel. Von Interesse sind Beziehungen zwischen je zwei dieser Winkel, die keinen gemeinsamen Scheitelpunkt haben.
Winkel an einander schneidenden Geraden
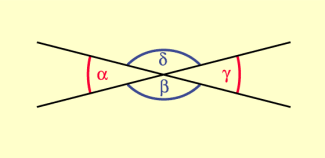
Schneiden einander zwei Geraden, so heißen die gegenüberliegenden Winkel Scheitelwinkel.
Im Bild 1 sind und sowie und Scheitelwinkel.
Scheitelwinkel sind immer gleich groß.
Es gilt:
-
Scheitelwinkel
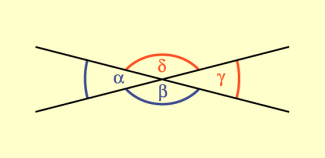
Schneiden einander zwei Geraden, so heißen immer zwei nebeneinanderliegende Winkel Nebenwinkel.
Nebenwinkel haben einen gemeinsamen Schenkel. Die beiden anderen Schenkel liegen auf ein und derselben Geraden und haben genau den Scheitelpunkt gemeinsam (Bild 2).
Die Winkelsumme zweier Nebenwinkel beträgt deshalb stets 180°:
Ergänzen sich zwei Winkel zu 180°, heißen sie Supplementwinkel.
Ergänzen sich zwei Winkel zu 90°, heißen sie Komplementwinkel.
Nebenwinkel sind ein Beispiel für Supplementwinkel. Darüber hinaus gibt es aber auch Supplementwinkel, die keine Nebenwinkel sind.
Winkel an geschnittenen Parallelen
Schneiden zwei verschiedene parallele Geraden eine dritte Gerade, so entstehen acht Winkel. Von Interesse sind Beziehungen zwischen je zwei dieser Winkel, die keinen gemeinsamen Scheitelpunkt haben.
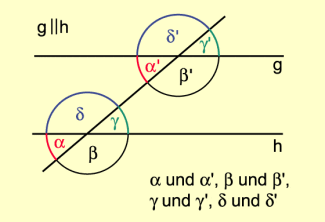
Stufenwinkelsatz
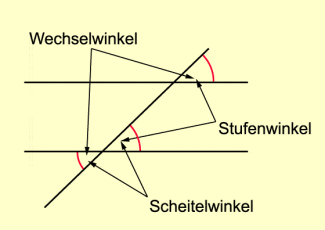
Stufenwinkel sind gleich groß genau dann, wenn sie an parallelen Geraden liegen (Bild 3).
Dieser Satz in der „...genau dann, wenn...“-Formulierung hat zwei Teile: Er sagt einerseits aus, dass an geschnittenen Parallelen die Stufenwinkel gleich groß sind.
Andererseits – und das ist die andere Richtung des Satzes – liefert er ein Kriterium, mit dem entschieden werden kann, ob zwei Geraden parallel sind: Sind die entsprechenden Stufenwinkel gleich, dann handelt es sich um parallele Geraden.
-
Stufenwinkel
Wechselwinkelsatz
Wechselwinkel sind gleich groß genau dann, wenn sie an parallelen Geraden liegen (Bild 4).
-
Wechselwinkel
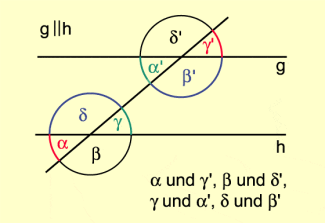
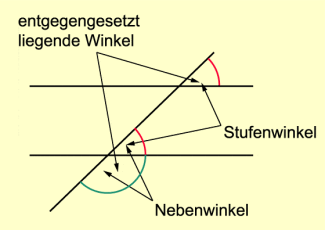
Satz über entgegengesetzt liegende Winkel
Entgegengesetzt liegende Winkel ergänzen sich zu genau dann, wenn sie an parallelen Geraden liegen (Bild 5).
-
Entgegengesetzt liegende Winkel
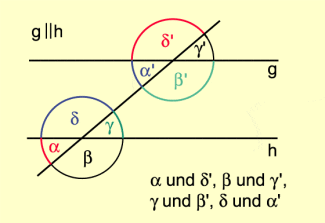
Zum Beweis muss zu allen drei Sätzen jeder der beiden Teile getrennt bewiesen werden (Bild 6).
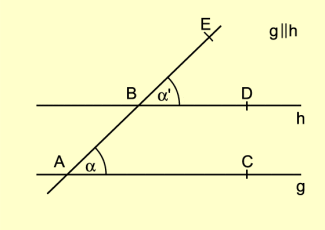
Beweis des Stufenwinkelsatzes:
Voraussetzung:
und sind Stufenwinkel an den Geraden g und h, die beide von der Geraden k geschnitten werden.
Behauptung:
Teil 1: Wenn.
Teil 2: Wenn .
Beweis zu Teil 1:
Wenn g || h, gilt bei der Verschiebung AB
- das Bild von A ist B,
- das Bild von g ist h (weil g || h),
- das Bild von k ist k (weil Verschiebung längs k),
- das Bild des Strahls AC ist der Strahl BD,
- das Bild des Strahls AB ist der Strahl BE.
Damit ist klar, dass bei der Verschiebung CAB auf DBE abgebildet wird und folglich gilt:
Beweis zu Teil 2:
Hier wird vorausgesetzt. Dann muss es eine Bewegung geben, die CAB auf DBE abbildet.
Weil die Strahlen AB und BE auf der gleichen Geraden k liegen und aufeinander abgebildet werden, muss k bei der Bewegung auf sich abgebildet werden, wobei insbesondere das Bild von A der Punkt B () sein muss.
Diese Forderung erfüllt nur die Verschiebung AB. Da jede Verschiebung Geraden parallel zu sich abbildet und nach Voraussetzung AC auf BD abgebildet wird, sind die Geraden g und h parallel.
-
Beweis des Stufenwinkelsatzes
Beweisideen zum Wechselwinkelsatz und zum Satz über entgegengesetzt liegende Winkel:
Der Wechselwinkelsatz kann auf den Stufenwinkelsatz zurückgeführt werden, indem noch der Satz über die Scheitelwinkel benutzt wird (Bild 7). (Der zu einem Winkel gehörige Wechselwinkel ist bekanntlich der Stufenwinkel seines Scheitelwinkels.)
-
Beweis des Wechselwinkelsatzes
Der Satz über entgegengesetzt liegende Winkel kann auf den Stufenwinkelsatz zurückgeführt werden, indem noch der Satz über die Nebenwinkel benutzt wird (Bild 8). (Der zu einem Winkel entgegengesetzt liegende Winkel ist bekanntlich Stufenwinkel eines seiner Nebenwinkel.)
-
Beweis des Satzes über entgegengesetzt liegende Winkel
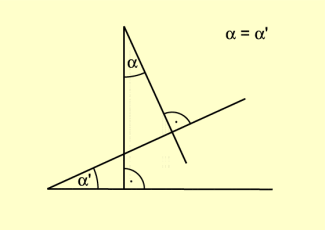
Winkel mit paarweise senkrecht aufeinanderstehenden Schenkeln
Zwei Winkel, deren Schenkel paarweise senkrecht aufeinander-stehen, sind gleich groß, falls der Scheitel des einen Winkels nicht im Inneren oder auf einem Schenkel des anderen Winkels liegt (Bild 9) .
-
Winkel mit paarweise senkrecht aufeinanderstehenden Schenkeln