Hyperbolische Funktionen
Mithilfe der e-Funktion lässt sich eine weitere Klasse von Funktionen definieren, die sogenannten hyperbolischen Funktion.
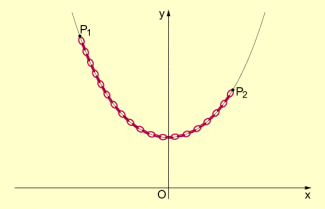
Unter diesen ist eine Funktion besonders hervorzuheben – der Cosinus hyperbolicus. Deren Graph hat die Form einer Kette, wenn man diese an ihren Enden aufhängt. Deshalb wird die entsprechende Kurve auch als Kettenlinie bezeichnet.
Unter Verwendung der Exponentialfunktion lassen sich weitere Funktionen, die sogenannten hyperbolischen Funktionen (bzw. Hyperbelfunktionen), definieren:
- Sinus hyperbolicus (bzw. Hyperbelsinus)
- Cosinus hyperbolicus (bzw. Hyperbelkosinus)
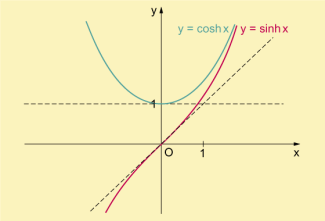
Die Graphen beider Funktionen sind in Bild 1 dargestellt.
-
Hyperbelsinus und Hyperbelkosinus
Entsprechend der bei den trigonometrischen Funktionen geltenden Beziehungen kann man noch ergänzen:
- Tangens hyperbolicus (bzw. Hyperbeltangens)
- Cotangens hyperbolicus (bzw. Hyperbelkotangens)
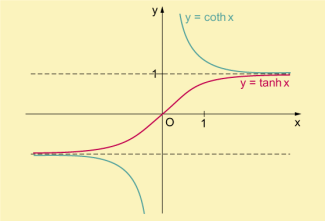
Bild 2 zeigt den Verlauf der Graphen des Hyperbeltangens und Hyperbelkotangens.
Die hyperbolischen Funktionen traten in ihren Grundlagen implizit u. a. bereits bei ISAAC NEWTON (1623 bis 1727) und bei ABRAHAM DE MOIVRE (1622 bis 1754) auf.
Die Theorie dieser Funktionen begründete der italienische Mathematiker VINCENZO RICCATI (1707 bis 1775) unter Verwendung geometrischer Betrachtungen. Im Jahre 1768 kam dann JOHANN HEINRICH LAMBERT (1728 bis 1777) auf die Idee, hyperbolische Funktionen für die Trigonometrie zu nutzen.
-
Hyperbeltangens und Hyperbelkotangens
Die Kettenlinie
Unter den oben definierten hyp erbolischen Funktionen ist eine besonders hervorzuheben – der Cosinus hyperbolicus. Wie aus Bild 1 zu erkennen ist, hat der Graph dieser Funktion die Form einer Kette, wenn man diese an ihren Enden aufhängt. Deshalb wird diese Kurve auch als Kettenlinie bezeichnet.
Das Problem, welche Kurve eine an ihren Ende aufgehängte Kette einnimmt (Bild 3), wurde erstmals von GALILEO GALILEI (1564 bis 1642) untersucht. GALILEI glaubte, dass es eine Parabel sei. Diese Annahme wurde vom deutschen Mathematiker, Physiker und Philosophen JOACHIM JUNGIUS (1587 bis 1657) in seiner 1639 erschienenen „Geometria empyrica“ widerlegt. Auch CHRISTIAAN HUYGENS (1629 bis 1695) wies den Fehler GALILEIs bei der Lösung nach, indem er zeigte, dass die Kettenlinie keine Parabel sein könne (und dies, wo doch selbst die päpstlichen Inquisition keinen Fehler im Werk GALILEIs gefunden hatte).
Mit dem Problem der Kettenlinie beschäftigten sich auch die Brüder JAKOB BERNOULLI (1654 bis 1705) und JOHANN BERNOULLI (1667 bis 1748) sowie der deutsche Gelehrte GOTTFRIED WILHELM LEIBNIZ (1646 bis 1716). Eine Lösung, d. h. die explizite Herleitung einer diese Funktion beschreibenden Gleichung, gelang im Jahre 1690.
-
Kettenlinie