Anwendung transzendenter Funktionen bei der Zinseszinsrechnung

Eine wichtige Anwendung transzendenter Funktionen ist die sogenannte Zinseszinsrechnung. Dabei wird davon ausgegangen, dass anfallende Zinsen in der Folgezeit mit verzinst werden.

Sind das Anfangskapital $K_0$, der Zinssatz p und der Zeitraum n (in Jahren) bekannt, so führt die Frage nach dem Endkapital $K_n$ auf die folgende Exponentialfunktion:
$K_n(n)=K_0\cdot {\left(\frac{100+p}{100}\right)}^n=K_0\cdot {\left(1+\frac{p}{100}\right)}^n$

Man setzt $1+\frac{p}{100}=q$ und nennt q den Zinsfaktor. Die Formel lautet dann:
$K_n(n)=K_0\cdot q^n$

Dabei wird davon ausgegangen, dass die Zinsen jährlich (p.a. – per annum) berechnet und jeweils am Endes des Jahres dem Kapital zugeschlagen werden.

Beispiel 1: Ein Betrag von 250 Euro wird auf acht Jahre fest angelegt und mit 4,5% p.a. verzinst. Wie groß ist das Endkapital?

Nach obiger Formel ergibt sich:
$K_8=250EUR\cdot {\mathrm{1,045}}^8\approx \mathrm{355,53}EUR$

Beispiel 2: Angenommen, zu Beginn unserer Zeitrechnung wäre einen Betrag von 1 (einer beliebig kleinen Einheit) zu 3% angelegt worden.
Welches Guthaben hätte sich daraus bis zum Jahr 2000 ergeben?

Nach obiger Formel erhält man:
$K_{2000}=1\cdot {\mathrm{1,03}}^{2000}\approx \mathrm{4,7255}\cdot {10}^{25}$

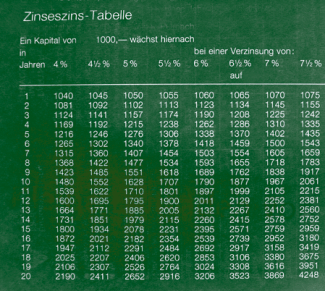
Nimmt man beispielsweise 1 Cent als Einheit, so wäre das ein Betrag von etwa 472550 Trillionen Euro (so viel Geld gibt es auf der ganzen Welt nicht).
Diese Aufgabe verdeutlicht das schnelle Wachstum bei exponentiellen Zusammenhängen.

Interessant ist die Frage nach dem Endkapital bei einer halbjährlichen Verzinsung. Es gilt dann:
$K_n(n)=K_0\cdot {\left(1+\frac{p}{2\cdot 100}\right)}^{2\cdot n}$

Beispiel 3: Ein Betrag von 250 Euro wird auf acht Jahre fest angelegt und mit 4,5% (p.a.) verzinst. Die Zinsen werden halbjährlich berechnet und dem Kapital zugeschlagen.

Nach obiger Formel ergibt sich
$K_8=250EUR\cdot {\mathrm{1,0225}}^{16}\approx \mathrm{356,90}EUR$
(also 1,38 EUR mehr als in Beispiel 1).

Geht man von einer monatlichen Verzinsung aus, gilt folgende Funktionsgleichung:
$K_n=K_0\cdot {\left(1+\frac{p}{12\cdot 100}\right)}^{12\cdot n}$

Beispiel 4: Ein Betrag von 250 Euro wird auf acht Jahre fest angelegt und mit 4,5% p.a. verzinst. Die Zinsen werden monatlich berechnet und dem Kapital zugeschlagen.

Nach obiger Formel ergibt sich
$K_8=250EUR\cdot {\mathrm{1,00375}}^{96}\approx \mathrm{358,09}EUR$
(also 2,57 EUR mehr als in Beispiel 1).

In Gedanken kann man dies fortsetzen und die Zeiten der Verzinsung immer kürzer, d.h. den Wert für a in folgender Formel immer größer, werden lassen:
$K_n=K_0\cdot {\left(1+\frac{p}{a\cdot 100}\right)}^{a\cdot n}$

Praktische Berechnungen werden nun schwierig, weil Taschenrechner und gängige Heimcomputer aufgrund ihrer eingeschränkten Genauigkeit beim Berechnen der Potenz ${\left(1+\frac{p}{a\cdot 100}\right)}^{a\cdot n}$ keine vernünftigen Ergebnisse mehr liefern.

Man erkennt indes, dass dem Problem der Grenzwert $\underset{a\to \infty }{\lim }{\left(1+\frac{1}{a}\right)}^a$ zugrunde liegt. Dieser liefert bekanntlich die eulersche Zahl e.

Für eine ständige unmittelbare Verzinsung würde daher die folgende Funktionsgleichung anwendbar sein:
$K_n=K_0\cdot \left(1+\frac{p}{100}\cdot e^n\right)$

Will man bei bekanntem Anfangs- und Endkapital und einer vorgegebenen Laufzeit den Zinssatz berechnen, ist die eingangs gegebene Formel nach q bzw. p umzustellen.

Es ergibt sich die folgende Wurzelfunktion:
$q(n)=\sqrt[n]{\frac{K_n}{K_0}}$
Hieraus lässt sich p folgendermaßen berechnen:
$p=(q-1)\cdot 100$

Beispiel 5: Für ein Darlehen von 1000 Euro muss man nach acht Jahren 1500 Euro zurückzahlen. Wie hoch ist der Zinssatz (p.a.)?

Man rechnet
$q=\sqrt[8]{\frac{1500EUR}{1000EUR}}=\sqrt[8]{\mathrm{1,5}}\approx \mathrm{1,051}989$,
woraus $p\approx \mathrm{5,1989}$ folgt. Der Zinssatz beträgt also rund 5,2%.

Ist im Zusammenhang mit der Zinseszinsrechnung nach der Zeit (der Anzahl der Jahre) gefragt, so muss man mit Logarithmusfunktionen arbeiten.
Umstellen der eingangs gegebenen Formel ergibt:
$n=\frac{{\log }_a{K}_n-{\log }_a{K}_0}{{\log }_{a}q}$
Anmerkung: Die Basis a ist beliebig wählbar. Im Folgenden wird mit dem natürlichen Logarithmus gerechnet.

Beispiel 6: Wie viele Jahre muss man einen Betrag von 250 Euro bei einem Zinssatz von 4,5% p.a. anlegen, um auf 800 Euro zu kommen?

Die Rechnung liefert das folgende Ergebnis:
$n=\frac{\ln 800-\ln 250}{\ln \mathrm{1,045}}\approx \mathrm{26,43}$

Im Allgemeinen wird man für n keine natürliche Zahl erhalten. Bei jährlicher Verzinsung muss man den Wert auf- bzw. abrunden und erhält dann mehr bzw. weniger als den für $K_n$ angesetzten Betrag. Im obigen Beispiel erhielte man für $n=27$ eine Endsumme von 820,50 Euro.

Beispiel 7: Nach welcher Zeit hat sich ein Anfangskapital bei einem Zinssatz von 3% bzw. 7% verdoppelt?

Mit $K_n=2$ und $K_0=1$ erhält man
$n=\frac{\ln 2-\ln 1}{\ln q}=\frac{\ln 2}{\ln q}$,
woraus sich für $q_3=\mathrm{1,03}$ und $q_7=\mathrm{1,07}$ die Werte $n_3\approx \mathrm{23,45}$ bzw. $n_7\approx \mathrm{10,24}$ ergeben.
Anmerkung: Auch hier gilt, dass man bei jährlicher Verzinsung runden muss und sich im Beispiel nach 23 bzw. zehn Jahren das Anfangskapital noch nicht ganz verdoppelt hat.

Oben ausgeführte Berechnungen lassen sich auch mithilfe einer Tabellenkalkulation ausführen.