Logarithmusfunktionen

Der Zerfall von radioaktivem Jod 131 wird durch die Funktionsgleichung $\text{m}\left(\text{x}\right)={\text{m}}_{\text{0}}\cdot {\left(\sqrt[\text{8}]{\frac{\text{1}}{\text{2}}}\right)}^{\text{x}}$ beschrieben. Dabei bedeuten ${\text{m}}_{\text{0}}$ die Ausgangsmasse und m(x) die vorhandene Masse nach x Tagen.

Will man ermitteln, nach wie vielen Tagen sich die Ausgangsmasse halbiert hat, so ist die Gleichung ${\text{m}}_{\text{0}}\cdot {\left(\sqrt[\text{8}]{\frac{\text{1}}{\text{2}}}\right)}^{\text{x}}=\frac{\text{1}}{\text{2}}{\text{m}}_{\text{0}}$ zu lösen, man muss also den Exponenten bei bekannter Basis und bekanntem Potenzwert bestimmen.
Es ist das Logarithmieren erforderlich:
Wenn $a^c=b$ dann ist $c={\log }_{a}b$.

Funktionen mit Gleichungen der Form
$\text{y}=\text{f}\left(\text{x}\right)={\text{log}}_{\text{a}}\text{x}\left(\text{a}\text{,}\text{x}\in ℝ\text{;}\text{a}\text{,}\text{x}>\text{0;}\text{a}\ne \text{1}\right)$
heißen Logarithmusfunktionen.

Die Logarithmusfunktion mit der Gleichung $\text{y}=\text{f(x)}={\text{log}}_{\text{a}}\text{x}$ ist die Umkehrfunktion der Exponentialfunktion mit y = g(x) = $a^x$.

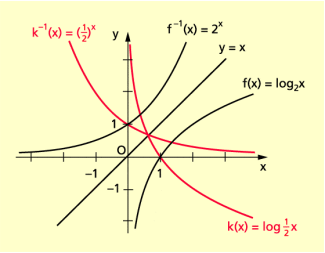
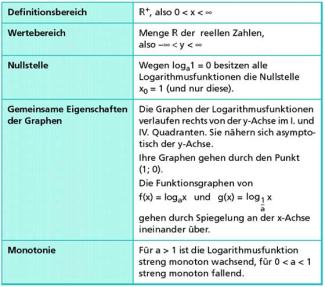
Logarithmusfunktionen besitzen die in der folgenden Übersicht aufgeführten Eigenschaften.

Rechnen mit Logarithmen

Für das Rechnen mit Logarithmen gelten eine Reihe von Regeln und Gesetzmäßigkeiten, die aus den Zusammenhängen zwischen Potenzieren und Logarithmieren sowie aus den Potenzgesetzen für Potenzen mit reellen Exponenten resultieren. Es gelten die im Folgenden angeführten Logarithmengesetze:

Sind x und y positive reelle Zahlen und ist a eine positive reelle Zahl mit $a\ne 1$, so gilt:
$\begin{array}{l}•{\log }_a\left(a^x\right)=x\\ •a^{{\log }_{a}y}=y\\ •{\log }_a\left(x\cdot y\right)={\log }_{a}x+{\log }_{a}y\\ •{\log }_a\left(\frac{x}{y}\right)={\log }_{a}x-{\log }_{a}y\\ •{\log }_a{x}^k=k\cdot {\log }_{a}x\left(k\in ℝ\right)\end{array}$
Speziell gilt: ${\log }_{a}1=0;{\log }_{a}a=1$

Man schreibt verkürzend:
${\log }_{10}x=\lg x$
${\log }_{e}x=\ln x$ und
${\log }_{2}x=\mathrm{ld}x$ (oder auch $\mathrm{lb}x$)

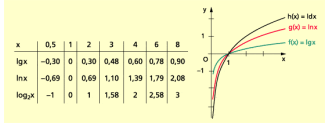
Die Graphen der Funktionen
$f\left(x\right)=\lg x$
$g\left(x\right)=\ln x$ und
$h\left(x\right)={\log }_{2}x$
sind in der folgenden Abbildung dargestellt.

Beispiele für das (vorteilhafte) Rechnen mit Logarithmen:

• $\begin{array}{c}\lg \left(\mathrm{6,3}\cdot \mathrm{0,5}\right)=\lg \mathrm{6,3}+\lg \mathrm{0,5}=\lg \mathrm{6,3}+\lg 1-\lg 2\\ =\lg \mathrm{6,3}-\lg 2\approx \mathrm{0,4983}\end{array}$
• $\lg 4+\lg 7-\lg 14=\lg \frac{4\cdot 7}{14}=\lg 2=\mathrm{0,3010}$
• $\begin{array}{c}\lg 16+\lg 625=\lg 2^4+\lg 5^4=4\lg 2+4\lg 5\\ =4\left(\lg 2+\lg 5\right)=4\cdot \lg \left(2\cdot 5\right)=4\cdot \lg 10=4\end{array}$

Von besonderer wissenschaftlicher und praktischer Bedeutung sind die Logarithmusfunktionen mit den Basen 10 und e sowie auch 2.