Kugelvolumen, Herleitung

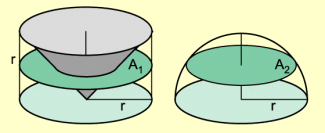
Zur Herleitung der Formel für das Volumen einer Kugel kann nach einer Idee von GALILEI ein Körper geschaffen werden, der in gleichen Höhen den gleichen Querschnitt wie eine Halbkugel hat. Ein solcher Körper entsteht, wenn man aus einem Kreiszylinder mit dem Grundflächenradius r und der Höhe r einen Kreiskegel mit gleicher Grundfläche und gleicher Höhe herausschneidet (Bild 1).

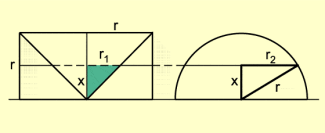
Werden dieser Restköper und eine Halbkugel mit dem gleichen Radius r in der gleichen Höhe x durch eine Ebene geschnitten, haben die Schnittflächen den gleichen Flächeninhalt, wie die folgende Überlegung an einem Schnitt durch beide Körper zeigt (Bild 2).

Da das hervorgehobene Dreieck gleichschenklig ist, gilt:
$r_1=x$

Für den Flächeninhalt $A_1$ des Kreisringes ergibt sich demzufolge:
$A_1=\pi r^2-\pi r_1{}^2=\pi r^2-\pi x^2=\pi \left(r^2-x^2\right)$

Nach dem Satz des Pythagoras gilt für die Halbkugel $r^2=x^2+r_2{}^2$ und deshalb$A_2=\pi r_2{}^2=\pi \left(r^2-x^2\right)$;
also ist $A_1=A_2$.

Nach dem Satz des Cavalieri gilt dann
$\begin{array}{l}{V}_{\text{Halbkuge}l}=V_{\text{Zylinder}}-V_{Kegel}\\ =\pi r^{2}h-\frac{1}{3}\pi r^{2}h=\frac{2}{3}\pi r^{2}h\end{array}$

und folglich gilt für das Volumen einer Kugel:
$V_{\text{Kuge}l}=\frac{4}{3}\pi r^{2}h$