Lineare Gleichungssysteme, Grafisches Lösen

Ein lineares Gleichungssystem mit den beiden Variablen x und y besteht aus zwei linearen Gleichungen (I und II) mit jeweils den Variablen x und y.
I     a 1 x + b 1 y = c 1     a 1 ,b 1 ,c 1 ∈ ℚ II       a 2 x + b 2 y = c 2       a 2 ,b 2 ,c 2 ∈ ℚ
Zur Lösungsmenge eines linearen Gleichungssystems gehören die Zahlenpaare, die sowohl zur Lösungsmenge der Gleichung I als auch zur Lösungsmenge der Gleichung II gehören.

Ein lineares Gleichungssytem mit den beiden Variablen x und y besteht aus zwei linearen Gleichungen (I und II) mit jeweils den Variablen x und y.
I     a 1 x + b 1 y = c 1     a 1 ,b 1 ,c 1 ∈ ℚ II       a 2 x + b 2 y = c 2       a 2 ,b 2 ,c 2 ∈ ℚ
Zur Lösungsmenge eines linearen Gleichungssystems gehören die Zahlenpaare , die sowohl zur Lösungsmenge der Gleichung I als auch zur Lösungsmenge der Gleichung II gehören.

Ein lineares Gleichungssystem mit zwei Variablen wird in folgenden Schritten zeichnerisch gelöst:

  1. Beide lineare Gleichungen werden in die Form y = mx + n gebracht.
  2. Die zugehörigen Geraden werden in dasselbe Koordinatensystem gezeichnet.
  3. Die Lösung entspricht den Koordinaten des Schnittpunktes der Geraden und wird aus der grafischen Darstellung abgelesen.

Lösungsmöglichkeiten:

  • Schneiden die beiden Geraden einander in einem Punkt, so hat das lineare Gleichungssystem genau eine Lösung.
  • Verlaufen die beiden Geraden parallel zueinander, so hat das lineare Gleichungssystem keine Lösung.
  • Gehört zu beiden Gleichungen ein und dieselbe Gerade, so hat das lineare Gleichungssystem unendlich viele Lösungen.

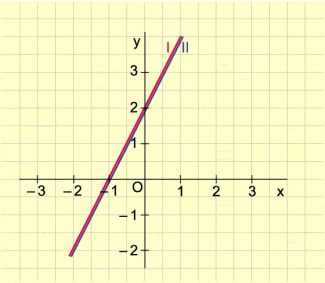
Beispiel 1 (Bild 1):

I   2x + 2y = 6     x ,   y ∈ ℚ II     2x + y = 5 I   a             y = − x + 3 IIa           y = − 2x + 5

Die Lösungen der Gleichung I sind Punkte der Geraden I.
Die Lösungen der Gleichung II sind Punkte der Geraden II.
Die Lösung des Gleichungssystems sind Punkte, die sowohl zur Geraden I als auch zur Geraden II gehören. Das ist nur der Punkt (2; 1).
Das lineare Gleichungssystem hat die Lösungsmenge
L = {   ( 2;   1 )   } , d. h. x = 2 und y = 1.

Grafische Lösung des linearen Gleichungssystems

Grafische Lösung des linearen Gleichungssystems

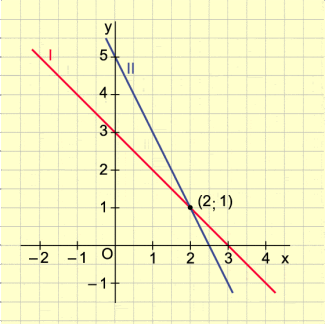
Beispiel 2 (Bild 2):

I         x + y = 3     x ,   y ∈ ℚ I I     2 x + 2 y = 4 I   a                 y = − x + 3 I I a               y = − x + 2

Die beiden Geraden schneiden einander nicht.
Es gibt keinen Punkt, der gleichzeitig zu beiden Geraden gehört.
Das Gleichungssystem hat keine Lösung: L = { } .
Das lässt sich bereits an den beiden umgeformten Gleichungen erkennen. Beide haben den gleichen Anstieg m = –1, die Geraden verlaufen also parallel.

Grafische Lösung des linearen Gleichungssystems

Grafische Lösung des linearen Gleichungssystems

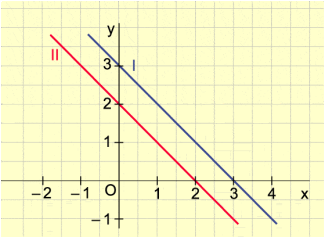
Beispiel 3 (Bild 3):

I         y − 2 x = 2     x ,   y ∈ ℚ II         2y − 4x = 4 I   a                   y = 2x + 2 IIa                 y = 2x + 2

Die beiden Geraden sind identisch.
Alle Punkte der Geraden sind Lösungen des linearen Gleichungssystems. Es gibt also unendlich viele Lösungen. Zur Lösungsmenge gehören alle die Zahlenpaare, welche die Gleichung y = 2x + 2 erfüllen.

Grafische Lösung des linearen Gleichungssystems

Grafische Lösung des linearen Gleichungssystems

Zahlenpaare parallel Berechnung lineares Gleichungssystem Mathcad identisch interaktives Rechenbeispiel Schnittpunkt Lösung Lösungsmenge
Lexikon Share
Mathe Note verbessern?
 

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

  • 40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
  • Hausaufgabenhilfe per WhatsApp
  • Original Klassenarbeiten mit Lösungen
  • Deine eigene Lern-Statistik
  • Kostenfreie Basismitgliedschaft
Mathe kostenlos lernen
Verwandte Artikel
alle anzeigen
Angaben zum Lexikon
Impressum
© Duden Learnattack GmbH, 2024

Einloggen