Mengenrelationen
Zwei Mengen sind gleich, wenn sie dieselben Elemente besitzen.
Zwei Mengen A und B sind gleichmächtig, wenn es eine umkehrbar eindeutige (eineindeutige) Abbildung gibt, bei der jedem Element der einen Menge genau ein Element der anderen Menge zugeordnet wird (Zeichen: A ~ B).
Die Menge A ist Teilmenge der Menge B, wenn jedes Element von A zugleich in B enthalten ist.
B heißt dann Obermenge von A.
Zwei Mengen sind gleich, wenn sie dieselben Elemente besitzen. (Beide Mengen müssen dieselben Elemente besitzen. Es genügt nicht, wenn es die gleichen Elemente sind!)
Beispiel:
Die Menge der geraden Primzahlen und die Menge aller natürlichen Lösungen der Gleichung sind gleich.
Zwei Mengen A und B sind gleichmächtig, wenn es eine umkehrbar eindeutige (eineindeutige) Abbildung gibt, bei der jedem Element der einen Menge genau ein Element der anderen Menge zugeordnet wird (Zeichen: A ~ B).
Endliche Mengen sind damit gleichmächtig, wenn sie die gleiche Anzahl von Elementen besitzen.
Beispiele:
- Die Menge der schwarzen und die Menge der weißen Figuren eines Schachspiels sind gleichmächtig.
- Die Menge der Tassen in einem vollständigen Kaffeeservice ist gleichmächtig der Menge der Untertassen.
- Die Menge der natürlichen Zahlen ist gleichmächtig der Menge der ganzen Zahlen: ~
Die Menge A ist Teilmenge der Menge B, wenn jedes Element von A zugleich in B enthalten ist .
B heißt dann Obermenge von A.
Beispiel:
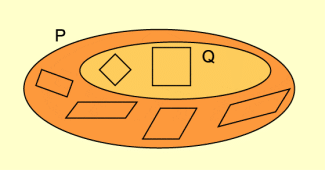
Q ist die Menge aller Quadrate. P die Menge aller Parallelogramme. , denn jedes Quadrat ist ein (spezielles) Parallelogramm.
Ist jedes Element von A zugleich in B enthalten und gibt es in B mindestens ein Element, welches nicht in A enthalten ist, dann ist A echte Teilmenge von B.
Beispiel:
Weil jedes Quadrat ein Parallelogramm ist, gilt .
Weil es zugleich auch (mindestens) ein Parallelogramm gibt, welches kein Quadrat ist, gilt sogar .
-
Teilmenge
Zwei Mengen A und B sind elementfremd (disjunkt), wenn sie kein gemeinsames Element besitzen.
Beispiel:
A ist die Menge der schwarzen Buben eines Skatspiels. B ist die Menge der roten Buben eines Skatspiels.
Diese Mengen sind disjunkt, da es keinen Buben im Skatspiel gibt, der sowohl rot als auch schwarz ist.
-
Disjunkte Mengen
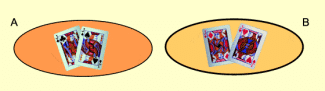
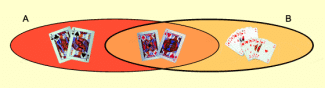
Zwei Mengen A und B sind überschnitten, wenn (jeweils mindestens)
- ein Element von A nicht in B ist,
- ein Element von B nicht in A ist und
- ein Element in A und B zugleich ist.
Beispiel:
A ist die Menge der Buben eines Skatspiels.
B ist die Menge der roten Karten eines Skatspiels.
Diese Mengen sind überschnitten, denn im Skatspiel gibt es eine rote Karte, die kein Bube ist, es gibt einen Buben, der nicht rot ist und es gibt einen roten Buben.
-
Überschnittene Mengen