Mathematik
Klasse
7-8
- Lexikon
- Mathematik
- 7 Planimetrie
- 7.6 Dreiecke
- 7.6.3 Besondere Linien und Punkte des Dreiecks
- Mittelsenkrechten im Dreieck
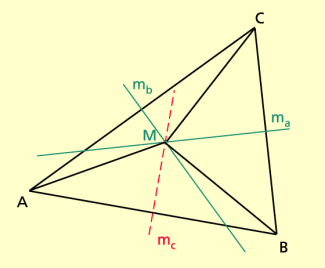
Mittelsenkrechten im Dreieck
Die Mittelsenkrechten eines Dreiecks sind die Mittelsenkrechten der Dreiecksseiten. Die drei Mittelsenkrechten schneiden einander in genau einem Punkt. Dieser Punkt ist der Mittelpunkt eines Kreises, auf dem alle Eckpunkte des Dreiecks liegen. Man nennt diesen Kreis den Umkreis des Dreiecks.
Beweis:
Voraussetzung:
Δ ABC ist ein beliebiges Dreieck; , und sind die Mittelsenkrechten der Seiten a, b und c. M ist der Schnittpunkt von und .
Behauptung:
M liegt auch auf .
Mittelsenkrechte und Umkreis eines Dreiecks
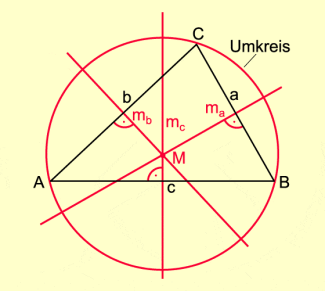
Beweis (Bild 2):
- Alle Punkte, die auf liegen, sind von B und C gleich weit entfernt.
M liegt auf , also ist .
- Alle Punkte, die auf liegen, sind von C und A gleich weit entfernt.
M liegt auf , also ist .
- Damit ist also auch
d. h., M ist von A und B gleich weit entfernt.
(Hiermit ist bereits klar, dass es zu jedem Dreieck einen Kreis durch alle drei Eckpunkte des Dreiecks gibt.)
Alle Punkte, die von A und B gleich weit entfernt sind, liegen auf . M liegt folglich auch auf . (w. z. b. w.)
Bei spitzwinkligen Dreiecken liegt der Punkt M innerhalb (Bild 1), bei stumpfwinkligen Dreiecken außerhalb des Dreiecks und bei rechtwinkligen Dreiecken auf der Hypotenuse. Im gleichschenkligen Dreieck liegt M auf der Symmetrieachse des Dreiecks, die auch Mittelsenkrechte ist.
Beweisfiguren
Material zum Thema
Ein Angebot von 