Geonext

Geonext – als Weiterentwicklung von Geonet – ist ein vollständig in die Internetumgebung eingebundenes interaktives Geometrieprogramm.
Während man mit statischen Programmen „nur“ zeichnen und konstruieren kann, lassen sich Konstruktionen von Polygonen oder Kreisen, die mit einer dynamischen Geometriesoftware (DGS) wie Geonext erzeugt wurden, stetig verändern. Mithilfe des sogenannten Zugmodus können Punkte und Geraden verschoben werden, ohne dass sich die damit verbundenen charakteristischen Eigenschaften der Konstruktion ändern. Größen wie Längen und Winkel lassen sich außerdem messen und mit Berechnungen verknüpfen.

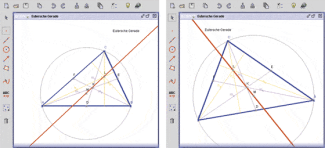
Eulersche Gerade (Bild 1)
Durch Konstruktion eines beliebigen Dreiecks lässt sich leicht zeigen, dass die Schnittpunkte der Seitenhalbierenden und der Dreieckshöhen und der Mittelpunkt des Umkreises auf einer Geraden ( eulersche Gerade ) liegen.

Durch Ziehen an den Eckpunkten lässt sich das einmal konstruierte Dreieck beliebig verändern. Der veranschaulichte geometrische Zusammenhang, die eulersche Gerade, bleibt dabei erhalten.

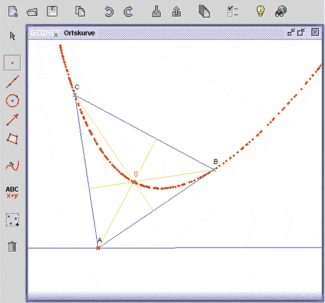
Ortskurve des Höhenschnittpunktes von Dreiecken (Bild 2)

Nachdem in einem beliebigen Dreieck der Höhenschnittpunkt konstruiert wurde, soll dessen Lageänderung bei Verschieben eines Eckpunktes entlang einer Geraden untersucht werden. Befindet sich der Höhenschnittpunkt im Spurmodus , so wird jede Lageänderung in Form einer Spur sichtbar gemacht. Es entsteht eine Ortskurve , in diesem Fall eine Parabel.

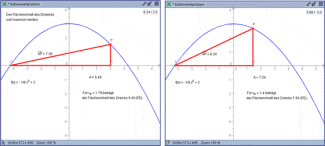
Experimentelle Bestimmung von Extremwerten (Bild 3)

Fortgeschrittene dynamische Geometriesysteme sind in der Regel mit einem Mess- und Rechenmodus ausgestattet. Dadurch können Abstände von Punkten und Größen von Winkeln gemessen, angezeigt und in mögliche Berechnungen eingebunden werden. Oftmals gestattet der Rechenmodus auch die Definition und grafische Darstellung von Funktionen. Durch die Verknüpfung beider dieser Eigenschaften können mit der DGS auch Extremwerte einer Funktion (bzw. einer Zielfunktion) experimentell ermittelt werden.

Dem Graphen der Funktion $f\left(x\right)=-x^2+3$ ist ein rechtwinkliges Dreieck derart einzubeschreiben, dass ein Eckpunkt mit einem Schnittpunkt des Graphen mit der x-Achse übereinstimmt, ein zweiter Eckpunkt beliebig auf dem Graphen von f und eine Kathete auf der x-Achse liegt. Aus der Menge aller möglichen Dreiecke ist das mit größtem Flächeninhalt gesucht.

Ist die Funktion grafisch dargestellt, kann ein Dreieck mit den genannten Bedingungen so eingezeichnet werden, dass ein Eckpunkt (P) auf dem Graphen frei beweglich ist. Durch eine vorher definierte Gleichung zur Berechnung des Flächeninhalts wird jede durch Verschieben von P hervorgerufene Änderung des Flächeninhalts unmittelbar angezeigt. Das gesuchte Dreieck mit größtem Flächeninhalt lässt sich dadurch näherungsweise bestimmen.