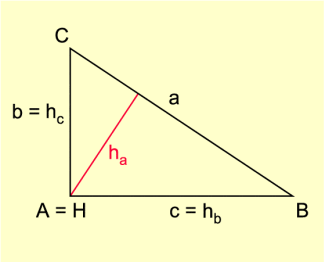
Höhen im Dreieck
Die Lotstrecken von den Eckpunkten auf die jeweilige Gegenseite (bei stumpfwinkligen Dreiecken auf deren Verlängerungen) heißen Höhen und werden mit h bezeichnet (Bild 1).
Es gilt der folgende Satz:
In einem Dreieck schneiden sich die drei Höhen in einem Punkt, dem Höhenschnittpunkt H.
Höhen im Dreieck
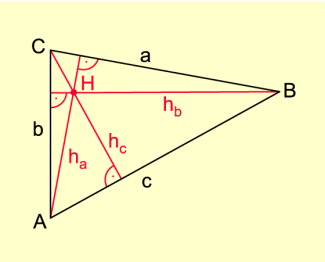
Beweis des Satzes:
Grundidee: Die Höhen sind, da sie senkrecht auf der jeweiligen Gegenseite stehen, parallel zu den Mittelsenkrechten, die sich in einem Punkt schneiden. Man sucht ein zweites Dreieck, in dem die Höhen des ersten die Mittelsenkrechten sind. Wenn das gelungen ist, ist die Aussage bewiesen.
- Konstruiere um Dreieck ABC aus den Parallelen zu den drei Seiten durch die jeweils gegenüberliegenden Eckpunkte ein Dreieck DEF (Bild 2).
- Es entstehen gemäß Kongruenzsatz wsw vier kongruente Dreiecke: ABC, BAD, ECB und CFA.
- A, B und C sind Mittelpunkte von , und .
, und sind sogenannte Mittelparallelen im Dreieck DEF. - Die Mittelsenkrechten im Dreieck DEF verlaufen also durch A, B bzw. C und stehen auch senkrecht auf , bzw. .
- Die innerhalb vom Dreieck ABC verlaufenden Abschnitte dieser Mittelsenkrechten sind die Höhen im Dreieck ABC.
(w. z. b. w.)
Beweisfigur
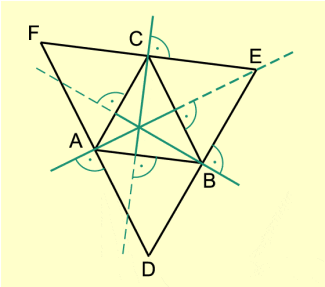
Dieser Beweis lässt sich auch bei stumpfwinkligen Dreiecken so führen. Dort liegt H außerhalb des Dreiecks (Bild 3).
Höhen im stumpfwinkligen Dreieck
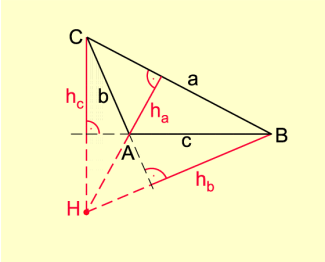
Der Höhenschnittpunkt im rechtwinkligen Dreieck ist der Scheitel des rechten Winkels (Bild 4).
Höhen im rechtwinkligen Dreieck
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 