Napierstäbchen
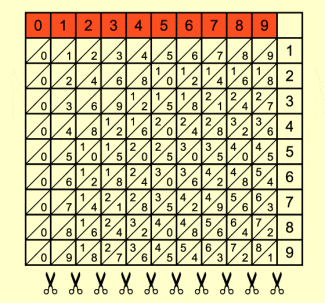
Bei seinen Untersuchungen des Multiplikationsalgorithmus fand JOHN NAPIER heraus, dass auch für die Multiplikation mehrstelliger Zahlen das kleine Einmaleins ausreicht, wenn man die Zwischenergebnisse geschickt addiert. Dazu änderte er die schon bekannte Einmaleins-Tafel so ab, dass die zu addierenden Zahlen leicht erfasst wurden. Der „Trick“ bestand darin, die Einmaleins-Produkte durch transversale Linien getrennt zu schreiben.
|
Einmaleins-Tafel |
Einmaleins-Tafel von NAPIER |
NAPIER verwendete dann Stäbchen aus Holz, die man variabel nebeneinander legen konnte und beschrieb sie nach obigem Prinzip mit dem kleinen Einmaleins. Mit diesen Rechenstäbchen schuf NAPIER ein erstes Hilfsmittel für die Multiplikation.
Multiplikation einer mehrstelligen Zahl mit einer einstelligen Zahl
Der mehrstellige Faktor wird gebildet, indem die entsprechenden Napierstäbchen nebeneinandergelegt werden. Als einstelliger Faktor kann das Stäbchen mit den natürlichen Zahlen von 1 bis 9 links oder rechts daneben gelegt werden. Das Produkt erhält man dann durch Addition der Teilprodukte der Zeile des einstelligen Faktors. Die Idee NAPIERs bestand also darin, die Multiplikation auf die einfachere Addition zurückzuführen. Diese Methode war so erfolgreich, dass noch um 1920 Rechenstäbchen als Schnittbogen gedruckt wurden, die ausgeschnitten als einfache Multiplikationshilfe dienten.
Der Grundgedanke der Napierstäbchen wurde von WILHELM SCHICKHARDT (1592 bis 1635) bei der Entwicklung seiner Rechenmaschine noch einmal aufgegriffen.
Beispiel 1:
Gelegte Napierstäbchen für
Beispiel 2::
Gelegte Napierstäbchen für
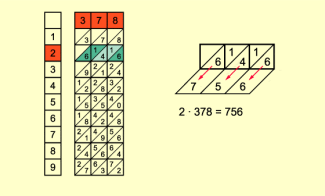
Gelegte Napierstäbchen für 2 · 378
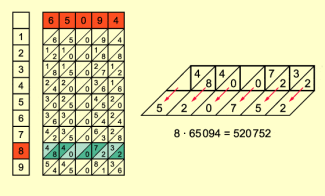
Gelegte Napierstäbchen für 8 · 65094
Multiplikation zweier mehrstelliger Zahlen
Eine einfache Variante besteht darin, einen der beiden mehrstelligen Faktoren nacheinander mit den Ziffern des anderen Faktors mithilfe der Napierstäbchen zu multiplizieren, die Teilprodukte um jeweils eine Stelle versetzt untereinanderzuschreiben und sie zu addieren, wie auch bei der schriftlichen Multiplikation üblich.
Beispiel 3:
Ein Bastelbogen „Napierstäbchen“ zum Ausdrucken, Ausschneiden und Ausprobieren ist in Bild 4 dargestellt.
Mit den Napierstäbchen wurde die Multiplikation auf die Addition zurückgeführt.
Bastelbogen für Napierstäbchen
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 