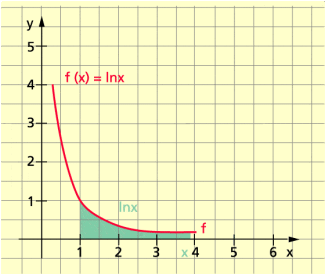
Natürliche Logarithmen

Logarithmen mit der Basis e (der eulerschen Zahl) heißen natürliche Logarithmen. Die Funktion $y=\ln x$ ist die Umkehrfunktion der Exponentialfunktion $y=e^x$.

In der Mathematik spielt die Zahl e eine fundamentale Rolle, unter anderem als Basis eines Logarithmensystems, der sogenannten natürlichen Logarithmen (wobei diesen gegenüber den dekadischen Logarithmen der Vorzug gegeben wird).

Für das praktische Rechnen brachten – solange man auf die Benutzung von Tabellen angewiesen war – die dekadischen Logarithmen Vorteile, weil für alle Zehnerpotenzen die Logarithmen durch die jeweiligen Zehnerpotenzen gegeben sind (z. B. $\lg 100=\lg {10}^2=2$). Diese gehen als Kennziffer in den Logarithmus ein, und die Mantissen sind unabhängig von Multiplikationen und Divisionen durch Zehnerpotenzen, so ist etwa:
$\lg 1234=\lg \left(\mathrm{0,1234}\cdot {10}^4\right)=\lg {10}^4+\lg \mathrm{0,1234}=4+\lg \mathrm{0,1234}$
Dieser praktische Gesichtspunkt ist aber für theoretische Untersuchungen von untergeordneter Bedeutung. Dort wird eine Basis vorgezogen, mit der einige theoretische Überlegungen und allgemeine Aussagen einfacher werden. Das leistet die Basis e, und das ist der Grund dafür, dass in der Wissenschaft natürliche Logarithmen vorgezogen werden. Durch das Hilfsmittel „Taschenrechner“ ist zu erwarten, dass dekadische Logarithmen auch für praktische Anwendungen an Bedeutung verlieren.

In höheren prozeduralen Programmiersprachen (PASCAL, C++ u. a.) sind Operatoren für das Potenzieren nicht enthalten. Ein Term wie $\sqrt[n]{x}$ muss deshalb mittels Exponential- und Logarithmusfunktion ausgedrückt werden:
$\sqrt[n]{x}=x^{\frac{1}{n}}=e^{\ln x^{\frac{1}{n}}}=e^{\frac{1}{n}\cdot \ln x}$

Noch ein interessanter Hinweis:
Die Maßzahl der Fläche unterhalb der Kurve 

$y=\frac{1}{x}$ im Intervall $\left[1;x\right]$ ist $y=\ln x$ (Bild 1).