- Lexikon
- Mathematik
- 3 Zahlen und Rechnen
- 3.1 Natürliche Zahlen
- 3.1.1 Zahlbegriff; Zahldarstellungen
- Natürliche Zahlen, Unendlichkeit
Natürliche Zahlen, Unendlichkeit
In der Menge der natürlichen Zahlen hat jede Zahl n einen (unmittelbaren) Nachfolger n + 1:
Der Nachfolger von 9 ist 10, der von 1.000.000 ist 1.000.001, der von 1.000.000.000.000.000 (eine Billiarde) ist 1.000.000.000.000.001 (eine Billiarde und eins).
Damit ist klar, dass es keine größte natürliche Zahl gibt.
Angenommen, jemand behauptet, er hätte die größte natürliche Zahl entdeckt, so bilde man den Nachfolger dieser Zahl und hat eine noch größere. Die Behauptung war also falsch.
Fängt man bei 1 an zu zählen, so kommt man nie zu einem Ende, es gibt unendlich viele natürliche Zahlen. Man sagt auch: Die Menge der natürlichen Zahlen ist unendlich.
Ein schönes Beispiel für diesen Sachverhalt ist folgendes:
- Man denke sich ein kosmisches Hotel mit unendlich vielen Einbettzimmern.
- Das Hotel ist voll belegt.
- Nun kommt noch ein Gast. Kann er in dem voll belegten Hotel noch untergebracht werden?
- Ja. Da es unendlich viele Zimmer gibt, rückt jeder Gast nur ein Zimmer weiter und das erste wird frei.
- Nach demselben Prinzip können natürlich auch noch 10 Gäste untergebracht werden.
- Auch unendlich viele Gäste können hier noch Platz finden, man muss das oben beschriebene Verfahren nur unendlich oft wiederholen.
Das Beispiel zeigt, dass man mit dem Begriff „Unendlich“ in der Mathematik sehr sorgfältig umgehen muss. Unendlich ist keinesfalls als eine Zahl aufzufassen, sondern als ein Prozess des Immer-und-so-weiter-Zählens bzw. Denkens beziehungsweise des Alle-Grenzen-Überschreitens. Unendlich ist deshalb auch nicht gleichbedeutend mit „unheimlich groß“.
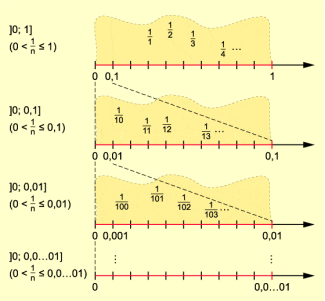
Auch die Menge der Stammbrüche mit hat unendlich viele Elemente:
Auf dem Zahlenstrahl liegen sie alle im Intervall .
Aber auch in den Teilintervallen liegen noch unendlich viele Stammbrüche (Bild 1).
Darstellung von Stammbrüchen in Intervallen
Ein Angebot von 