Polarkoordinatensystem

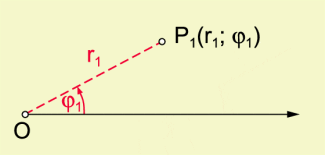
Ein Polarkordinatensystem besteht aus einem festen Punkt O, dem Pol (Anfangspunkt), sowie einer von diesem Punkt ausgehenden Halbgeraden, der Polarachse als Nullrichtung (Bild 1). Auf dieser Achse können (wie auf dem Zahlenstrahl) entsprechende Längen abgetragen bzw. gemessen werden.

Ein beliebiger Punkt P der Ebene lässt sich dann eindeutig durch Angabe folgender Koordinaten festlegen:

• den (positiven) Abstand r des Punktes P vom Pol;
• den Winkel $\varphi$, um den der Zahlenstrahl im mathematisch positiven Sinne gedreht werden muss, damit er durch P geht.
  (Dieser Winkel $\varphi$ wird auch Phase, Amplitude oder Anomalie genannt.)

Für die Polarkoordinaten r und $\varphi$ gilt:
$\begin{array}{l}0\le r<\infty \\ 0°\le \varphi <360°(bzw.0\le \varphi <2\pi )\end{array}$

Anmerkung: Für $x=y=0$ ist der Winkel $\varphi$ nicht definiert, für $x=0,y\ne 0$ ist $\varphi =\pm \frac{\pi }{2}$.

Mithilfe obiger Gleichungen kann man Polarkoordinaten in kartesische Koordinaten (und umgekehrt) umwandeln. Man spricht dann von einer sogenannten Koordinatentransformation.