Polygone
Polygone (Vielecke) sind abgeschlossene ebene Streckenzüge (Polygonzüge) aus endlich vielen Strecken. Ein Polygon ist eine ebene Figur, die durch Strecken begrenzt wird, wie Dreieck, Viereck, Fünfeck, Sechseck usw.
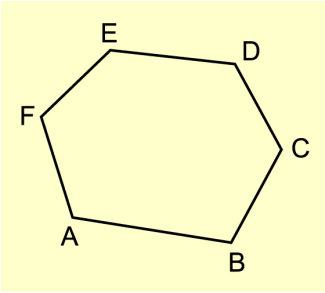
Polygone ( Vielecke) sind abgeschlossene ebene Streckenzüge (Polygonzüge) aus endlich vielen Strecken (Bild 1). Ein Polygon ist eine ebene Figur, die durch Strecken begrenzt wird, wie Dreieck, Viereck, Fünfeck, Sechseck usw.
Die Anzahl der Seiten eines Polygons ist stets gleich der Anzahl der Ecken. Die Vielecke werden nach der Anzahl n ihrer Ecken auch n-Ecke genannt.
-
Polygon
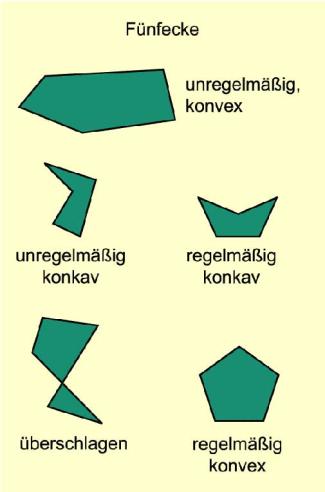
Sind die Seiten eines Polygons alle gleich lang und alle Innenwinkel zwischen benachbarten Seiten gleich groß, so heißt es regelmäßiges Polygon. Anderenfalls ist es ein unregelmäßiges Polygon (Bild 2).
Liegt jede Verbindungsstrecke zweier Eckpunkte des Polygons im Inneren (als Diagonale) oder auf dem Rand (als Seite), dann ist das Polygon konvex. Es hat keinen Innenwinkel, der größer als ist.
Anderenfalls ist das n-Eck konkav und besitzt mindestens einen Innenwinkel, der größer als ist.
Schneiden sich zwei Seiten, so heißt das Polygon überschlagen.
-
Fünfecke
Winkelsumme im Polygon
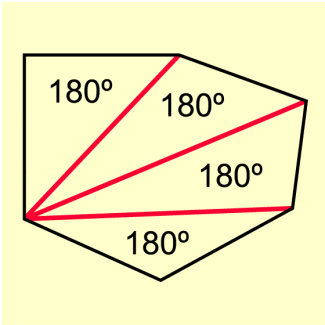
Ein (konvexes) n-Eck kann in (n – 2) Dreiecke zerlegt werden (Bild 3).
Für die Innenwinkelsumme eines beliebigen n-Ecks ergibt sich:
-
Winkelsumme
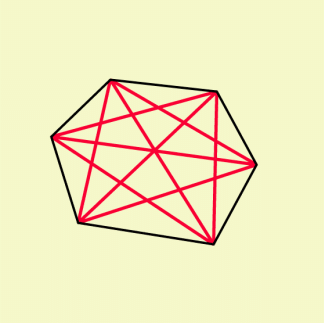
Anzahl der Diagonalen
Von jeder Ecke eines Polygons lassen sich zu den (n – 3) nicht benachbarten Eckpunkten Diagonalen zeichnen (Bild 4).
Das sind n · (n – 3) Verbindungsstrecken, wobei allerdings jede Strecke doppelt gezählt wurde.
Für die Anzahl d der Diagonalen im Polygon gilt:
Flächeninhalt eines Polygons
Der Flächeninhalt jedes Polygons lässt sich durch Zerlegung in Teildreiecke oder andere Teilfiguren berechnen. Dabei sind mehrere Varianten möglich:![]()
Es ist in Abb. (1):
Es ist in Abb. (2):
Es ist in Abb. (3):
-
Diagonalenanzahl