Wurzeln, Wissenswertes und Historisches
Eine Umkehrung des Potenzierens ist das Radizieren (Wurzelziehen).
Es ist die Frage nach dem Wert von a zu beantworten, wenn in der Potenz die Werte von b und c bekannt sind.
ist gleichbedeutend mit
(gesprochen: a ist gleich n-te Wurzel aus c).
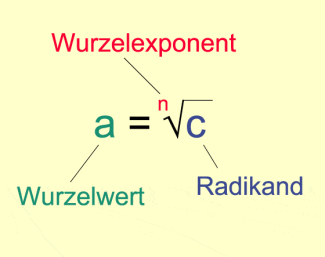
Dabei heißen n der Wurzelexponent, c der Radikand und a der Wurzelwert.
Eine Umkehrung des Potenzierens ist das Radizieren (Wurzelziehen).
Es ist die Frage nach dem Wert von a zu beantworten, wenn in der Potenz die Werte von b und c bekannt sind.
ist gleichbedeutend mit
(gesprochen: a ist gleich n-te Wurzel aus c).
Dabei heißen n der Wurzelexponent, c der Radikand und a der Wurzelwert.
Da b und c nicht allgemein vertauschbar sind, gibt es eine weitere Umkehrung, nämlich die Frage nach dem Exponenten b.
Dies führt zum Logarithmus.
Die Wurzel wurde ursprünglich, z. B. von LEONARDO FIBONACCI (1170 bis 1240), noch mit dem Buchstaben r vor der Zahl ( als r2) geschrieben. Das r ist die Abkürzung des Wortes radix (lat. Wurzel). Daher stammen auch die Begriffe radizieren und Radikand.
MICHAEL STIFEL (1487 bis 1567) stilisierte dieses r zu dem heute gebräuchlichen Wurzelhaken .
-
a ist gleich der n-ten Wurzel aus c
RENE DESCARTES (1596 bis 1650) führte den Querstrich über dem Radikanden ein, um z. B. unterscheiden zu können.
Wurzeln aus negativen Zahlen existieren im Bereich der reellen Zahlen nicht.
Beispiel:
Die Gleichung hat im Bereich der reellen Zahlen keine Lösung. Das Bild der Funktion ist eine nach oben geöffnete Parabel, die ihren tiefsten Punkt im Scheitel S (0; 2) hat und die x-Achse nicht schneidet.
Will man auch negative Wurzeln berechnen, muss man den Bereich der reellen Zahlen nochmals erweitern.
Man setzt und erhält sogenannte komplexe Zahlen
z = a + bi, die aus einem Realteil a und einem Imaginärteil bi bestehen (imaginär – franz.: nur angenommen, nicht wirklich). Die Bezeichnung rührt daher, dass man bereits im 16. Jahrhundert mit imaginären Größen wie mit Zahlen rechnete, ohne deren Bedeutung genau zu kennen.
Die Bezeichnung i für wurde im Jahre 1777 von LEONHARD EULER benutzt, setzte sich aber erst durch die Arbeiten des Mathematikers CARL FRIEDRICH GAUSS (1777 bis 1855) allgemein durch.
Der Bereich der komplexen Zahlen, lässt sich nicht mehr auf einer Zahlengeraden darstellen, da jedem Punkt dieser Zahlengeraden umkehrbar eindeutig eine reelle Zahl zugeordnet ist. Man kann die komplexen Zahlen aber in einer Ebene, der sogenannten gaußschen Zahlenebene darstellen. Dabei entspricht die waagerechte Achse der Zahlengeraden und eine dazu senkrechte Achse dient der Darstellung der imaginären Zahlen. Damit ist dann jedem Punkt dieser Ebene umkehrbar eindeutig eine komplexe Zahl zugeordnet.
Im Bereich der komplexen Zahlen gilt dann, der ebenfalls von GAUSS bewiesene Fundamentalsatz der Algebra. Dieser besagt, dass eine Gleichung n-ten Grades genau n Lösungen hat.

