Akustischer und optischer DOPPLER-Effekt
Der österreichische Physiker CHRISTIAN DOPPLER (1803-1853) entdeckte 1842, dass zwischen der von einem Beobachter wahrgenommenen Tonfrequenz und der Bewegung einer Schallquelle ein Zusammenhang besteht. Dieser Effekt wird als akustischer DOPPLER-Effekt bezeichnet.
Ein analoger Effekt tritt bei Licht auf. Er wird optischer oder relativistischer DOPPLER-Effekt genannt.
Der akustische DOPPLER-Effekt
Sind eine Schallquelle und ein Beobachter zueinander in Ruhe, so registriert der Beobachter genau die Frequenz (Tonhöhe), die von der Schallquelle abgegeben wird. Bei einer Relativbewegung zwischen Schallquelle und Beobachter ist ein anderer Effekt festzustellen.
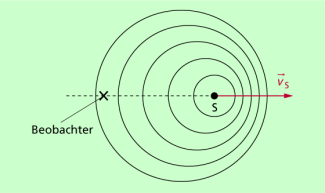
Der österreichische Physiker CHRISTIAN DOPPLER (1803-1853) entdeckte 1842, dass zwischen der von einem Beobachter wahrgenommenen Tonhöhe, die durch die Frequenz bestimmt wird, und der Bewegung einer Schallquelle ein Zusammenhang besteht. Diesen Effekt, der als akustischer DOPPLER-Effekt bezeichnet wird, kann man auch im Alltag leicht feststellen: Fährt z.B. ein hupendes Auto vorbei, so ist der Ton der Hupe beim Annähern des Autos höher als beim Entfernen. Die Deutung kann auch so erfolgen, wie es in Bild 1 dargestellt ist.
In Abhängigkeit davon, ob sich der Beobachter oder die Schallquelle bewegen, kann man verschiedene Fälle unterscheiden und auch mathematisch beschreiben.
| Die Schallquelle bewegt sich und der Empfänger (Beobachter) ruht | |
| Beim Annähern gilt: | Beim Entfernen gilt: |
größere Frequenz, höherer Ton | kleinere Frequenz, tieferer Ton |
| Der Empfänger (Beobachter) bewegt sich und die Schallquelle ruht | |
| Beim Annähern gilt: | Beim Entfernen gilt: |
größere Frequenz, höherer Ton | kleinere Frequenz, tieferer Ton |
| Dabei bedeuten: | |
Der optische DOPPLER-Effekt
DOPPLER selbst vertrat die Auffassung, dass der vom ihm entdeckte Effekt auch im optischen Bereich gilt. Diese Vermutung lag nahe, denn die Ausbreitung von Lichtwellen in einem Äther wurde als Analogie zur Ausbreitung von Schallwellen in Luft gedeutet. Ein experimenteller Nachweis konnte zu dieser Zeit nicht erbracht werden. Eine Erklärung für den optischen DOPPLER-Effekt lieferte erst die spezielle Relativitätstheorie. Deshalb ist auch die Bezeichnung relativistischer DOPPLER-Effekt üblich.
Im Unterschied zum akustischen DOPPLER-Effekt, der sich auf Schallwellen bezieht, handelt es sich bei Licht um elektromagnetische Wellen. Bei ihnen existiert, wie wir heute wissen, kein Trägermedium. Es ist auch kein ausgezeichnetes Bezugssystem vorhanden, relativ zu dem sich eine Phasengeschwindigkeit angeben lässt. Ausschlaggebend sind nur die Relativgeschwindigkeit zwischen Lichtquelle (Sender) und Beobachter (Empfänger) sowie die Lichtgeschwindigkeit. Es gelten die folgenden Beziehungen:
| Annähern von Sender und Empfänger | Entfernen von Sender und Empfänger |
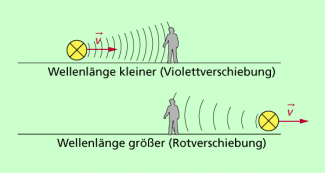
höhere Frequenz, kleinere Wellenlänge, Violettverschiebung | niedrigere Frequenz, größere Wellenlänge, Rotverschiebung |
| Dabei bedeuten: | |
Unter Nutzung der Gleichung
erhält man Gleichungen für die Wellenlänge, die vom Empfänger registriert wird:
| Beim Annähern von Sender und Empfänger | Beim Entfernen von Sender und Empfänger |
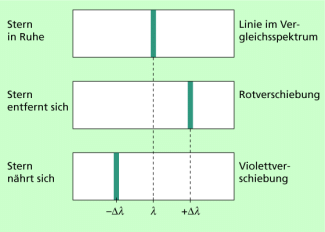
Violettverschiebung und Rotverschiebung
Beim Annähern von Sender und Empfänger wird vom Empfänger im Vergleich mit einer ruhenden Quelle eine Verschiebung von Spektrallinien in Richtung kleinerer Wellenlänge registriert. Da im Bereich des sichtbaren Lichtes das violette Licht die kleinste Wellenlänge hat, spricht man von einer Violettverschiebung, also einer Verschiebung in Richtung Violett.
Beim Entfernen von Sender und Empfänger wird vom Empfänger im Vergleich mit einer ruhenden Quelle eine Verschiebung von Spektrallinien in Richtung größerer Wellenlänge registriert. Man spricht deshalb von einer Rotverschiebung. Nicht verwechselt werden darf diese Rotverschiebung mit der Beeinflussung von Frequenzen bzw. Wellenlänge durch Gravitationsfelder, die mitunter als relativistische Rotverschiebung bezeichnet wird und nur im Rahmen der allgemeinen Relativitätstheorie erklärt werden kann.
Entdeckung und Bedeutung der Rotverschiebung
Entdeckt wurde die Verschiebung von Spektrallinien in Richtung Rot im Jahre 1929 durch den amerikanischen Astronomen EDWIN POWELL HUBBLE (1889-1953). HUBBLE untersuchte die Spektren von Galaxien und stellte dabei fest, dass die bekannten Spektrallinien verschiedener Elemente durchweg in Richtung größerer Wellenlängen verschoben waren.
Als Rotverschiebung wird in der Astronomie folgender Term festgelegt:
Unter Nutzung der oben genannten Gleichung für die Wellenlänge beim Entfernen von Sender und Empfänger voneinander kann man auch schreiben:
Stellt man die Gleichung nach der Geschwindigkeit v um, so erhält man eine Gleichung für die Geschwindigkeit, mit der sich eine Lichtquelle vom Beobachter entfernt. Die Geschwindigkeit wird in der Astronomie deshalb als Fluchtgeschwindigkeit bezeichnet. Für die Fluchtgeschwindigkeit gilt:
Rotverschiebung in der Astronomie
Die Rotverschiebung von Spektrallinien ermöglicht es, die Bewegung von Galaxien und Quasaren genauer zu charakterisieren. Quasare wurden 1963 entdeckt. Es sind wahrscheinlich die Kerne junger Galaxien. Sie senden eine starke Radiostrahlung aus. Astronomische Untersuchungen haben ergeben:
Bei allen Galaxien tritt eine Rotverschiebung auf. Das bedeutet: Sie entfernen sich von uns, wobei die Fluchtgeschwindigkeit mit der Entfernung zunimmt. Für den Zusammenhang zwischen der Fluchtgeschwindigkeit und der Entfernung gilt das Gesetz von HUBBLE:
Die größten bisher gemessenen Rotverschiebungen treten bei Quasaren auf. So wurde im Jahre 2000 ein Quasar mit einer Rotverschiebung von 5,8 entdeckt. Hier verschiebt sich die LYMAN- - Linie des Wasserstoffs, die im Labor eine Wellenlänge von 121,6 nm hat, zu 829,3 nm. Damit ergibt sich für diesen Quasar eine Fluchtgeschwindigkeit von 0,96 c oder 96 % der Lichtgeschwindigkeit.
Suche nach passenden Schlagwörtern
- Rotverschiebung
- Violettverschiebung
- Berechnung
- Dopplereffekt
- Empfänger
- Wellenlänge
- relativistischer Doppler-Effekt
- Astronomie
- Fluchtgeschwindigkeit
- EDWIN POWELL HUBBLE
- Spektrallinien
- Frequenz
- akustischer Doppler-Effekt
- Simulation
- Quasare
- Sender
- Rechenbeispiel
- Doppler-Effekt
- optischer Doppler-Effekt
- relativistische Rotverschiebung