- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.9 Statik und Dynamik von Flüssigkeiten und Gasen
- 2.9.1 Hydro- und Aerostatik
- Auftrieb und Auftriebskraft
Auftrieb und Auftriebskraft
Befindet sich ein Körper in einer Flüssigkeit oder in einem Gas, so verringert sich scheinbar seine Gewichtskraft. Das kann man experimentell einfach nachweisen, indem man einen Körper an einem Federkraftmesser befestigt, seine Gewichtskraft bestimmt und den Körper anschließend ins Wasser taucht. Am Federkraftmesser wird dann eine deutlich kleinere Kraft als die Gewichtskraft angezeigt. In der Flüssigkeit bzw. in dem Gas muss also der Gewichtskraft des Körpers eine Kraft entgegenwirken. Diese Kraft nennt man Auftriebskraft
, die Erscheinung selbst Auftrieb.
Ursache des Auftriebs
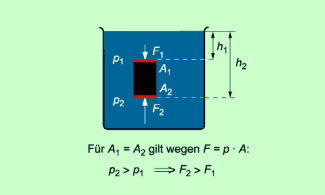
Ursache für die Entstehung des Auftriebs ist der unterschiedlich große Schweredruck p in verschiedenen Tiefen h (Bild 2).
Das archimedische Gesetz
Die Auftriebskraft an einem Körper ist umso größer, je größer sein eingetauchtes Volumen ist. Gleichzeitig verdrängt der eingetauchte Körper mit seinem Volumen ein genauso großes Volumen Flüssigkeit. Die verdrängte Flüssigkeit hat eine bestimmte Gewichtskraft, die umso größer ist, je größer ihr Volumen ist. Damit ergibt sich ein Zusammenhang zwischen der Auftriebskraft an einem Körper und der Gewichtskraft der von ihm verdrängten Flüssigkeit bzw. des verdrängten Gases. Dieser Zusammenhang wird durch das archimedische Gesetz beschrieben. Es lautet:
Für einen Körper, der sich in einer Flüssigkeit oder in einem Gas befindet, gilt: Die auf den Körper wirkende Auftriebskraft ist gleich der Gewichtskraft der von ihm verdrängten Flüssigkeits- bzw. Gasmenge.
Dieses Gesetz wurde zuerst von ARCHIMEDES von Syrakus
(287 v. Chr. - 212 v. Chr.) entdeckt. Die Gewichtskraft der verdrängten Flüssigkeit ist von deren Masse abhängig. Die Masse einer Flüssigkeit oder eines Gases ist wiederum von Dichte und Volumen abhängig, sodass man auch formulieren kann:
Die Auftriebskraft ist umso größer,
- je größer das verdrängte Flüssigkeits- oder Gasvolumen ist und
- je größer die Dichte des verdrängten Stoffes ist.
Diese Zusammenhänge lassen sich auch in Form einer Gleichung darstellen. Für die an einen Körper angreifende Auftriebskraft in Flüssigkeiten und Gasen gilt:
Bedeutung des Auftriebs
Die Bedeutung des Auftriebs besteht vor allem darin, dass von ihm abhängig ist, ob ein Körper in Wasser oder in Luft sinkt, schwebt, steigt oder schwimmt. Das spielt in vielen Bereichen von Natur, Technik und Alltag eine Rolle, was die nachfolgenden Beispiele zeigen.
Für Fische ist es günstig, wenn sie unter Wasser schweben, also weder von selbst nach oben steigen noch nach unten sinken. Das wird durch die Schwimmblase erreicht. In ihr befindet sich soviel Luft, das die Auftriebskraft genauso groß ist wie die Gewichtskraft.
Bei Schiffen muss die Konstruktion so erfolgen, dass sie sicher schwimmen. Damit das der Fall ist, muss die Auftriebskraft so groß sein, dass das Schiff auch bei voller Beladung genügend weit aus dem Wasser ragt.
Beim Schwimmen in verschiedenen Gewässern kann man feststellen, dass der Auftrieb davon abhängig ist, ob das Wasser salzhaltig ist oder nicht. In Salzwasser ist der Auftrieb deutlich größer als in Süßwasser. Das Schwimmen fällt dort leichter. Das hängt damit zusammen, dass die Dichte von Salzwasser größer ist als die von Süßwasser und damit bei gleichem Körpervolumen die Auftriebskraft in Salzwasser größer ist als die in Süßwasser.
Auch für den Transport von Samen, das Fliegen von Heißluftballons und Luftschiffen, das Fahren von U-Booten oder das Tauchen ist der Auftrieb von entscheidender Bedeutung.
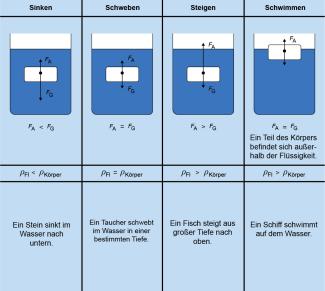
Sinken, Schweben, Steigen und Schwimmen von Körpern
Je nachdem, wie groß die Gewichtskraft eines Körpers und die an ihm in entgegengesetzter Richtung wirkende Auftriebskraft sind, kann der Körper in einer Flüssigkeit oder in einem Gas sinken, schweben, steigen oder schwimmen. Die Auftriebskraft ist gleich der Gewichtskraft der vom Körper verdrängten Flüssigkeits- oder Gasmenge (archimedisches Gesetz).
- Ein Körper sinkt nach unten, wenn die Gewichtskraft größer als die Auftriebkraft ist.
Beispiel: Blatt Papier in Luft. - Ein Körper schwebt in einer bestimmten Tiefe bzw. Höhe, wenn die Gewichtskraft genauso groß wie die Auftriebkraft ist.
Beispiel: Fisch in einer bestimmten Tiefe. - Ein Körper steigt nach oben, wenn die Gewichtskraft kleiner als die Auftriebkraft ist.
Beispiel: Ball, den man unter Wasser drückt. - Ein Körper schwimmt, wenn die Gewichtskraft genauso groß wie die Auftriebkraft ist, wobei sich ein Teil des Körpers außerhalb der Flüssigkeit befindet.
Beispiel: Schlauchboot oder Luftmatratze
Die Bedingungen für das Sinken, Schweben, Steigen oder Schwimmen von Körpern kann man auch mithilfe der Dichten der Körper und der Flüssigkeit bzw. des Gases beschreiben. Dazu sind folgende Überlegungen durchzuführen: Die Gewichtskraft eines Körpers ist von seiner Masse und diese wiederum von seiner Dichte und seinem Volumen abhängig.
Es gilt:
Die Gewichtskraft des verdrängten Stoffes und damit die Auftriebskraft ist von der Dichte und dem Volumen des betreffenden Stoffes, z. B. Wasser oder Luft, abhängig.
Es gilt:
Da das Volumen des eingetauchten Körpers und das des verdrängten Stoffes gleich sind, ist für das Verhältnis der beiden Kräfte zueinander die Dichte des Körpers und die Dichte des Stoffes entscheidend dafür, ob ein Körper sinkt, schwebt, steigt oder schwimmt. Dabei ist zu beachten, dass für den Körper immer die mittlere Dichte betrachtet werden muss.
So schwimmt z. B. ein Schiff aus Stahl mit einer schweren Ladung deshalb, weil seine mittlere Dichte kleiner ist als die das Wassers. Zwar hat Stahl und sicher auch die Schiffsladung eine größere Dichte als Wasser, aber man muss beachten, dass sich im Schiff auch viele Hohlräume mit Luft befinden, sodass die mittlere Dichte eines Schiffes kleiner ist als die von Wasser.
Alle Zusammenhänge sind in Bild 5 im Überblick dargestellt.
Es sind auch Beispiele genannt. Die Formulierungen und Beispiele beziehen sich auf Wasser. Sie gelten aber auch für beliebige andere Flüssigkeiten und für Gase, insbesondere auch für die Luft.
Auftrieb und Auftriebskraft
Sinken, schweben, steigen, schwimmen
© Duden Learnattack GmbH
Ein Angebot von 