Bezugssysteme
Was ist ein Bezugssystem?
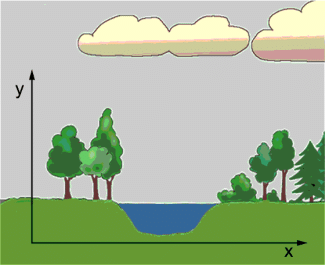
Zur Kennzeichnung des Ortes oder der Bewegung von Körpern ist ein Koordinatensystem erforderlich, das zumeist mit einem bestimmten Bezugskörper verbunden ist (Bild 1).
Ein Koordinatensystem mit dem entsprechenden Bezugskörper bezeichnet man als Bezugssystem.
In Bild ist ein solches Bezugssystem dargestellt, bei dem die Erdoberfläche als Bezugskörper gewählt ist.
Als Bezugskörper wählt man häufig die Erdoberfläche oder einen fest mit ihr verbundenen Körper (z.B. Baum, Berg). Das mit diesem Körper verbundene Koordinatensystem ermöglicht es, den Ort eines Körpers durch Angabe von Koordinaten genau zu charakterisieren. Im dargestellten Fall lässt sich die Lage eines Körpers in der x-y-Ebene angeben.
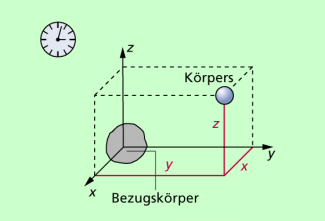
Will man die Bewegung eines Körpers im Raum eindeutig kennzeichnen, so ist ein räumliches Koordinatensystem erforderlich, so wie das in Bild 2 dargestellt ist. Darüber hinaus benötigt man auch noch eine Uhr, um z.B. den zeitlichen Ablauf von Bewegungen erfassen zu können.
Räumlich kann man die Lage eines Körpers auch mithilfe eines Ortsvektors erfassen. Ein solcher Ortsvektor ist ein Vektor, der vom Ursprung des Koordinatensystems bis zum betreffenden Körper verläuft.
In einem räumlichen Koordinatensystem wird der jeweilige Ort eines Körpers durch die betreffenden Koordinaten x, y und z gekennzeichnet.
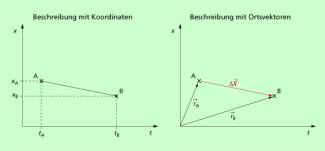
In der Physik verzichtet man meist auf die relativ komplizierte räumliche Betrachtung und beschränkt sich auf eine Raumrichtung und die Zeit. Damit erhält man einfach zu überschauende Sachverhalte, die sich auch mathematisch gut beschreiben und grafisch veranschaulichen lassen (Bild 3). Damit lassen sich insbesondere Ortsveränderungen (Bewegungen) relativ einfach beschreiben. Statt mit Ort-Zeit-Diagrammen arbeitet man häufig mit Weg-Zeit-Diagrammen, Geschwindigkeits-Zeit-Diagrammen oder Beschleunigung-Zeit-Diagrammen.
Ruhe und Bewegung
Die Antwort auf die Frage, ob sich ein Körper bewegt oder ob er in Ruhe ist, hängt von der Wahl des Bezugssystems ab.
Ein Körper ist in Bewegung, wenn er seine Lage gegenüber einem Bezugssystem verändert. Er ist in Ruhe, wenn er seine Lage gegenüber einem Bezugssystem nicht ändert. Jede Bewegung ist somit relativ und kann nur gegenüber einem Bezugsystem angegeben werden. Man spricht deshalb auch von der Relativität der Bewegung bzw. der Ruhe.
Häufig ist das gewählte Bezugsssystem ein mit der Erdoberfläche verbundenes Koordinatensystem. Es kann aber auch ein beliebiges anderes Bezugssystem gewählt werden. Sitzt man z. B. in einem fahrenden Zug still, so ist man sowohl in Ruhe als auch in Bewegung. Gegenüber dem Zug ist man in Ruhe, denn man ändert seine Lage gegenüber dem Zug nicht. Gleichzeitig fährt aber der Zug mit hoher Geschwindigkeit auf den Gleisen entlang. Gemeinsam mit dem Zug ändert man seine Lage, z. B. gegenüber den Häusern an der Bahnstrecke (Bild 2).
Lange wurde in der Physik die Frage diskutiert, ob es ein absolut ruhendes Bezugssystem (einen absoluten Raum) gäbe, also ein bevorzugtes Bezugssystem. ALBERT EINSTEIN hat in der speziellen Relativitätstheorie gezeigt, dass es weder einen absoluten Raum noch eine absolute Zeit gibt. Genauere Informationen dazu sind unter den betreffenden Stichwörtern zu finden.
Unbeschleunigte Bezugssysteme
In der Physik ist zwischen unbeschleunigten und beschleunigten Bezugssystemen zu unterscheiden.
Ein Bezugssystem, in dem das newtonsche Trägheitsgesetz gilt, nennt man unbeschleunigtes Bezugssystem oder Inertialsystem, abgeleitet von inertia (lat.) = Trägheit. In solchen Inertialsystemen lassen sich die viele physikalische Gesetze, z.B. die Bewegungsgesetze, besonders einfach formulieren. Für solche unbeschleunigten Koordinatensysteme gilt:
Es gibt kein bevorzugtes Inertialsystem. Alle Inertialsysteme sind gleichberechtigt.
Jedes Bezugssystem, das sich zu einem Inertialsystem gleichförmig und geradlinig bewegt, ist ebenfalls wieder ein Inertialsystem.
Die Beschreibung von Bewegungen in einem Inertialsystem kann relativ einfach für ein anderes Inertialsystem umgerechnet werden. Die dazu erforderliche Koordinatentransformation wird als GALILEI-Transformation bezeichnet. Genauere Informationen dazu findet man unter dem betreffenden Stichwort.
Zu beachten ist: Ein mit der Erdoberfläche verbundenes Koordinatensystem kann nur näherungsweise als Inertialsystem angesehen werden, da die Erde um ihre Achse rotiert und damit jeder Punkt der Erdoberfläche eine beschleunigte Bewegung ausführt.
Beschreibung der Bewegung eines Körpers in einem Ort-Zeit-Diagramm mit Koordinaten (Bild links) oder mit Ortsvektoren (Bild rechts)
Beschleunigte Bezugssysteme
Jeder hat mit beschleunigten Bezugssystemen schon Erfahrungen gesammelt: In einem bremsenden Bus muss man sich festhalten, um nicht nach vorn zu fallen, beim Anfahren wirkt eine Kraft nach hinten. Bei einem Kettenkarussell wirkt eine Kraft radial nach außen.
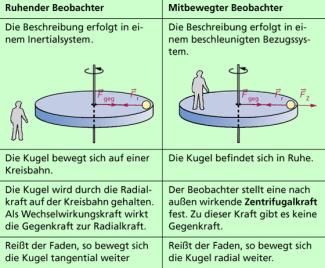
Ein Bezugssystem, das fest mit einem Körper verbunden ist, der sich beschleunigt bewegt, wird als beschleunigtes Bezugssystem bezeichnet. Bild 4 zeigt dafür ein Beispiel.
Bezugssysteme und Relativitätstheorie
Die Auseinandersetzung mit der von ISAAC NEWTON (1643-1727) postulierten absoluten Zeit und dem absoluten Raum führten Anfang des 20. Jahrhunderts zu neuen Vorstellungen von Raum und Zeit, die ALBERT EINSTEIN (1879-1955) zusammenfassend in der speziellen Relativitätstheorie (SRT) formulierte. Das führte auch zu veränderten Auffassungen über Bezugssysteme. Genauere Informationen findet man im Abschnitt „Relativitätstheorie“ unter solchen Stichwörtern wie Raum und Zeit in der SRT, Grundaussagen der SRT, galileisches Relativitätsprinzip und LORENTZ-Transformation.
Die Kreisbewegung eines Körpers kann von einem Inertialsystem (ruhendem Bezugssystem) oder von einem beschleunigten Bezugssystem (mitrotierendem System) aus beschrieben werden.
Koordinatensystem galileisches Relativitätsprinzip Albert Einstein Isaac Newton Lorentz-Transformation Zeit spezielle Relativitätstheorie Ruhe Raum beschleunigtes Bezugssystem unbeschleunigtes Bezugssystem Galilei-Transformation Inertialsystem Bezugskörper Ortsvektor Relativität von Bewegung Bewegung Bezugssysteme Relativität von Ruhe
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 