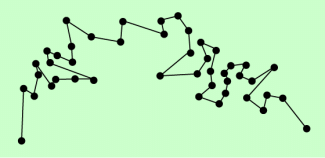
Brownsche Bewegung

Die unregelmäßige Bewegung von mikroskopisch beobachtbaren Körperchen wird als brownsche Bewegung bezeichnet.

Man nennt sie auch brownsche Molekularbewegung. Benannt ist diese Erscheinung nach dem schottischen Biologen ROBERT BROWN (1773-1858), der im Jahre 1827 Blütenstaub unter einem Mikroskop untersuchte. Dabei fiel ihm die unregelmäßige Bewegung der Staubkörnchen auf. Zuerst glaubte er, dass es sich bei den Bestandteilen der Pollenkörner um Mikroorganismen handelt, erkannte dann aber, dass die beobachtete Bewegung auch bei Ruß- und Staubkörner vorliegt. Des Weiteren konnte er feststellen, dass die Geschwindigkeit der Teilchen abhängig ist von deren Masse ist: Je geringer die Teilchenmasse, desto stärker ist bei einer bestimmten Temperatur ihre Bewegung.

Die brownsche Bewegung kommt folgendermaßen zustande: Die auch mikroskopisch nicht sichtbaren Teilchen (Atome, Moleküle), aus denen eine Flüssigkeit oder ein Gas aufgebaut ist, befinden sich in ständiger Bewegung. Sie stoßen dabei an die viel größeren, im Mikroskop sichtbaren Blütenstaubkörnchen oder an Rauchteilchen und schieben diese unregelmäßig hin und her. Diese unregelmäßige Bewegung kann man im Mikroskop beobachten.

Die brownsche Bewegung ist damit ein Beleg für die Existenz kleinster, nicht sichtbarer Teilchen und dafür, dass sich diese Teilchen (Atome, Moleküle) bewegen. Sie ist damit auch ein experimenteller Beleg für das Teilchenmodell und für die Existenz von Atomen.

ROBERT BROWN selbst konnte die von ihm beobachtete Erscheinung nicht erklären. Das gelang erst 1905 dem berühmten deutschen Physiker ALBERT EINSTEIN (1879-1955), der darüber hinaus auch die mittlere Verschiebung $\overline{x}$ eines Teilchens angeben konnte. Die mittlere quadratische räumliche Verschiebung eines Teilchens beträgt:

$\overline{x^2}=\frac{k\cdot T\cdot t}{2\cdot \pi \cdot \eta \cdot r}$

Die Herleitung dieser Gleichung soll hier nicht dargestellt werden. Die Abhängigkeit der einzelnen Größen von der Verschiebung kann jedoch durch einfache Überlegungen nachvollzogen werden. Aus der kinetischen Gastheorie ist die mittlere kinetische Energie eines Teilchens bekannt. Es gilt:

$E_{kin}=\frac{3}{2}k\cdot T$

Aus der Mechanik wissen wir, dass die kinetische Energie eines Teilchens $E_{\text{kin}}=\frac{1}{2}m\cdot \overline{v^2}$ beträgt. Gleichsetzen der beiden Beziehungen ergibt, dass die mittlere quadratische Geschwindigkeit $\overline{v^2}$ eines Teilchens proportional zur Temperatur und zur BOLTZMANN-Konstanten k ist:

$\frac{1}{2}\cdot m\cdot \overline{v^2}=\frac{3}{2}\cdot k\cdot T$

Da Geschwindigkeit und Strecke proportional zueinander sind, ist der Term $k\cdot T$ im Zähler des Bruches der von EINSTEIN angegebenen Gleichung einzusehen. Im Nenner steht unter anderem die dynamische Viskosität $\eta$ des Stoffes, d.h. je zäher der Stoff ist, desto geringer ist die Verschiebung. Dies ist sicherlich richtig, da sich die Widerstandskraft mit zunehmender Zähigkeit ebenfalls erhöht.
Gleiches gilt auch für die Größe des Teilchens. Bei wachsender Zeit kann sich das Teilchen immer weiter von seinem ursprünglichen Ort wegbewegen, was uns die Zeit im Zähler unserer Beziehung verstehen lässt.

Bereits im Altertum nahmen einige Gelehrte an, dass alle Stoffe aus kleinsten Teilchen bestehen, die nicht mehr zerteilt werden können. Diese Teilchen nannten sie Atome (vom griechischen Wort atomos: das Unteilbare). Diese Idee geriet später in Vergessenheit. Die Untersuchungen solcher Erscheinungen wie der brownschen Bewegung bestätigten später die Richtigkeit der Teilchenvorstellung und untermauerten die Auffassung von der Existenz vonAtomen und Molekülen.