Carnotscher Kreisprozess

Der Carnotsche Kreisprozess, bestehend aus je zwei isothermen und adiabatischen Zustandsänderungen, repräsentiert die „Takte“ einer ideal arbeitenden Wärmekraftmaschine. Dabei wird das Arbeitsmittel als ideales Gas betrachtet und die Prozessführung als reversible angenommen.

1. Takt: Durch Aufnahme von Wärme erfolgt eine isotherme Expansion. Es wird die Arbeit verrichtet.
2. Takt: Bei einer adiabatischen Expansion verringert sich die Temperatur. Hierbei wird von dem Gas arbeitet verrichtet, seine innere Energie verringert sich.
3. Takt: Für die isotherme Kompression muss Arbeit zugeführt werden. Die dabei entstehende Wärme wird an die Umgebung abgegeben.
4. Takt: Durch eine adiabatische Kompression wird die Temperatur erhöht und damit der Ausgangszustand wieder erreicht.

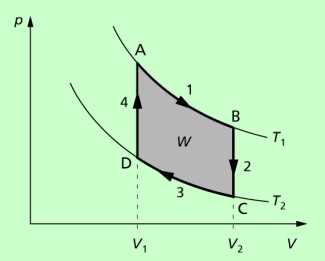
Nach dem 1. Hauptsatz der Thermodynamik ist die abgegebene mechanische Arbeit gleich der Änderung der Wärme in dem System. Die von den Zustandskurven eingeschlossene Fläche ist ein Maß für die abgegebene Arbeit.

Veränderung der Aggregatzustände

#Teilchenmodell #Atome #Aggregatzustände #Wechselwirkungen

Der Aggregatzustand

#Stoffeigenschaften #Aggregatzustand #Teilchenmodell #Löslichkeit #Modelle

Kreisprozesse bei Wärmekraftmaschinen

Die Umwandlung von Wärme in mechanische Arbeit ist von großer wirtschaftlicher Bedeutung. Wird doch durch diesen Prozess die Energieform qualitativ so verändert, dass sie unmittelbar in Produktionsprozessen nutzbar ist. Dabei wird in Kauf genommen, dass ein Teil der zur Verfügung stehenden inneren Energie für die Umwandlung benötigt wird. Wie groß dieser Anteil ist und wie er verringert werden kann, war und ist eine zentrale Frage beim Bau von Wärmekraftmaschinen.

Die ersten Maschinen zur Umwandlung von thermischer in mechanischer Energie waren Dampfmaschinen. In ihnen wird der als Arbeitsmittel verwendete Wasserdampf nacheinander in immer wiederkehrende Zustände überführt. Einen solcher Prozess, in dem der Ausgangszustand stets wieder erreicht wird, nennt man Kreisprozess.
Die Arbeitsweise der Dampfmaschinen war Vorlage für die theoretischen Untersuchungen des französischen Ingenieurs und Physikers SADI CARNOT (1796-1832). In seiner berühmten Schrift „Betrachtungen über die bewegende Kraft des Feuers und die zur Entwicklung dieser Kraft geeigneten Maschinen“ zeigte er,

warum eine Dampfmaschine mechanische Arbeit verrichten kann und
wodurch ihr Wirkungsgrad bestimmt wird.

ÉMILE CLAPEYRON (1799-1864), ein Schulfreund von S. CARNOT, stellte den Kreisprozess der Dampfmaschine durch je zwei Isothermen und Adiabaten in einem p-V-Diagramm dar (Bild 1). Dabei wird der Dampf als ideales Gas betrachtet und die Prozessführung als reversible angenommen. Dieser Kreisprozess ist heute als carnotscher Kreisprozess bekannt. Er ist gut geeignet, die Funktionsweise von Energiewandlern zu erklären. Es ist darüber hinaus der Kreisprozess, der den höchsten Wirkungsgrad aufweist.

Der carnotsche Kreisprozess

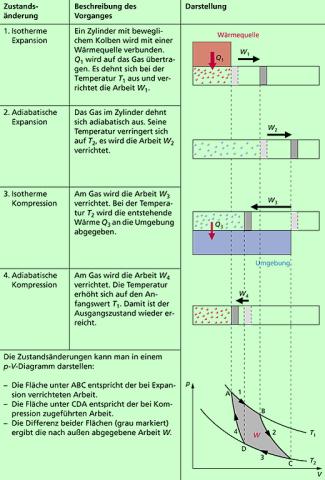
CARNOT untersuchte den beschriebenen Prozess genauer. Eine Wärmekraftmaschine, die einen solchen Kreisprozess durchläuft, bezeichnet man auch als CARNOT-Maschine. CARNOT unterteilte den Kreisprozess in vier Teilprozesse. Sie sind ausführlich in Bild 2 dargestellt und nachfolgend erläutert:

(1) Isotherme Expansion: Im Ausgangspunkt A hat das als Arbeitsmittel genutzte Gas
$\begin{array}{l} die hohe Temperatur T_{1}, den höchsten Druck p_{1} \\ und das kleinste Volumen V_{1} . \end{array}$
Um eine isotherme Expansion, also eine Vergrößerung des Volumens bei konstanter Temperatur, zu realisieren, muss dem Gas eine Wärme $Q_{1}$ zugeführt werden. Diese wird einem heißen äußeren Wärmespeicher entnommen. Beim Übergang in den Zustand B vergrößert das Gas sein Volumen. Es wird Arbeit verrichtet. Dabei verringert sich der Druck.
Die Zustandsgleichung für die isothermen Expansion eines idealen Gases lautet:

$p_{1} \cdot V_{1} = p_{2} \cdot V_{2}$

Die für die Zustandsänderung zugeführte Wärme ist
$Q_{1} = N \cdot k \cdot T_{1} \cdot \ln \frac{V_{2}}{V_{1}}$

(2) Adiabatische Expansion: Im Punkt B wird die Wärmezufuhr gestoppt. Das Gas dehnt sich aber weiterhin aus und kühlt sich dabei auf die Temperatur $T_{2}$ ab. Im Zustand C erreicht das Gas den kleinsten Druck und sein größtes Volumen. Die dabei verrichtete Arbeit führt zu einer Verringerung der inneren Energie des Gases. Der Kolben befindet sich im Umkehrpunkt.
Die Zustandsgleichung der adiabatischen Expansion des idealen Gases ist

$\begin{array}{l} p_{2} \cdot V_{2}^{κ} = p_{3} \cdot V_{3}^{κ} \\ Dabei ist κ der Adiabatenexponent . \end{array}$

(3) Isotherme Kompression: Beim Übergang von C nach D wird bei konstanter Temperatur $T_{2}$ das Volumen des Gases auf $V_{1}$ verringert. Dabei erhöht sich der Druck. Für diesen Teilprozess muss Arbeit aufgewendet werden. Die dabei entstehende Wärme $Q_{2}$ wird an einen kalten äußeren Wärmespeicher (die Umgebung) abgeführt.
Die Zustandsgleichung der isothermen Kompression des idealen Gases lautet:

$p_{3} \cdot V_{3} = p_{4} \cdot V_{4}$

Die dabei abgegebene Wärme ist:

$Q_{2} = N \cdot k \cdot T_{2} \cdot \ln \frac{V_{3}}{V_{4}}$

(4) Adiabatische Kompression: Im Punkt D ist die Wärme $Q_{2}$ abgegeben. Das Gas wird aber weiter komprimiert, bis das Ausgangsvolumen erreicht ist. In diesem Teilprozess erhöht sich der Druck und die Temperatur steigt wieder auf $T_{1}$ . Für die Realisierung dieses Teilprozesses muss ebenfalls Arbeit aufgewendet werden, die die innerer Energie des Gases erhöht. Der Kolben befindet sich im zweiten Umkehrpunkt, dem Ausgangspunkt A.
Die Gleichung für die adiabatische Kompression lautet:

$p_{4} \cdot V_{4}^{κ} = p_{1} \cdot V_{1}^{κ}$

Bei den adiabatischen Zustandsänderungen erfolgt jeweils eine Änderung der inneren Energie des Gases, die zu einer Erniedrigung bzw. zu einer Erhöhung der Temperatur führt.

Nach dem 1. Hauptsatz der Thermodynamik ist die abgegebene mechanische Arbeit W gleich der Änderung der Wärme in dem System. Die nach außen abgegebene Arbeit W ergibt sich aus der Differenz der zugeführten und abgegebenen Wärme bei den isothermen Teilprozessen:

$W = Q_{1} - Q_{2}$

Dabei gilt für die Wärmen $Q_{1} > Q_{2}$ , da die isotherme Expansion bei höherer Temperatur erfolgt als die isotherme Kompression.
Dies ist die Ursache, warum Dampfmaschinen, Verbrennungsmotoren und andere Wärmekraftmaschinen in der Lage sind, mechanische Arbeit zu verrichten. Die von den Isothermen und Adiabaten eingeschlossenen Fläche ist ein Maß für die nach außen abgegebene Arbeit. Sie kann durch Vergrößerung der Temperatur- und Volumendifferenzen verändert werden.

Der Wirkungsgrad beim carnotschen Kreisprozess

Wie groß die der Wirkungsgrad beim carnotschen Kreisprozess ist, lässt sich ebenfalls ermitteln. Der Wirkungsgrad ist das Verhältnis von abgegebener mechanischer Arbeit W zu zugeführter Wärme $Q_{1}$ .
Setzt man die entsprechenden Größen in die Gleichung für den Wirkungsgrad ein, so erhält man:

$η = \frac{Q_{1} - Q_{2}}{Q_{1}} = 1 - \frac{Q_{2}}{Q_{1}}$

Für den als reversibel angenommenen Prozess ergibt sich für das ideale Gas im carnotschen Kreisprozess:

$η = 1 - \frac{T_{2} \cdot \ln (V_{3} / V_{4})}{T_{1} \cdot \ln (V_{2} / V_{1})}$

Die Verhältnisse der Volumen können aus den Zustandsgleichungen der Teilprozesse ermittelt werden. Es ist:

$\frac{V_{2}}{V_{1}} = \frac{V_{3}}{V_{4}}$

Für den Wirkungsgrad einer CARNOT-Maschine ergibt sich damit:

$η = 1 - \frac{T_{2}}{T_{1}} = \frac{T_{1} - T_{2}}{T_{1}}$

Er ist also nur von der Temperaturdifferenz des Prozessablaufs abhängig. Da es in der Natur und in der Technik keine vollkommen reversibel ablaufende Prozesse gibt, ist dies der höchstmögliche Wirkungsgrad, der beim Umwandeln von thermischer in mechanischer Energie erreicht werden kann.

Beispiel: Eine Dampfmaschine, deren heißer Wärmespeicher siedendes Wasser bei Normdruck von 373 K enthält und deren kalter Wärmespeicher gefrierendes Wasser von 273 K beinhaltet, hat demnach einen Wirkungsgrad von:

$η = \frac{373 K - 273 K}{373 K} = 0,27$

Das ist ein erstaunlich niedriger Wert. Um diesen Wert zu erhöhen, muss die Temperaturdifferenz vergrößert werden. Technisch wird das durch ein Überhitzen des Wasserdampfes auf mehr als 500 K erreicht. Dabei wird das Wasser unter hohem Druck zum Sieden gebracht und der entstehende Dampf bei entsprechend hohem Druck in die Dampfturbinen eingeleitet. Dadurch werden in Kraftwerken bei der Erzeugung von Elektroenergie aus fossilen Brennstoffen Wirkungsgrade von bis zu 45 % erreicht.
Die Wirkungsgrade bei den Verbrennungsmotoren, die für Fahrzeuge genutzt werden (Dieselmotoren, Ottomotoren) liegen in der Regel deutlich niedriger.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen