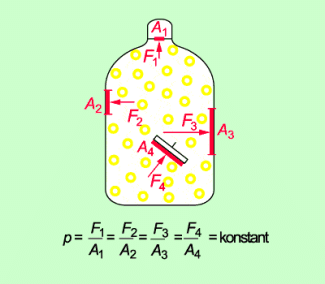Der Druck
Der Druck gibt an, mit welcher Kraft ein Körper auf eine Fläche von einem Quadratmeter wirkt.
| Formelzeichen: | p |
| Einheit: | ein Pascal (1 Pa) |
Der Druck kann allgemein berechnet werden mit der Gleichung:
Ein Pascal (1 Pa) ist die Abkürzung für die Einheit ein Newton je Quadratmeter. Benannt ist die Einheit nach dem französischen Mathematiker und Physiker BLAISE PASCAL (1623-1662).
Druck kann in Flüssigkeiten und in Gasen auftreten. Auch feste Körper können auf andere Körper Druck ausüben.
Im Alltag wird der Begriff Druck u. a. im Zusammenhang mit dem Reifendruck, dem Druck in Wasserleitungen oder dem Luftdruck verwendet. Dabei benutzt man den Begriff Druck häufig, um Wirkungen von Kräften zu beschreiben. Die physikalischen Größen Kraft und Druck müssen aber deutlich voneinander unterschieden werden. Während die Kraft angibt, wie stark ein Körper auf einen anderen einwirkt, beschreibt der Druck die Wirkung einer Kraft auf eine bestimmte Fläche. Allgemein gilt:
Der Druck gibt an, mit welcher Kraft ein Körper auf eine Fläche von einem Quadratmeter wirkt.
| Formelzeichen: | p |
| Einheit: | ein Pascal (1 Pa) |
| Berechnung: | F wirkende Kraft A Fläche, auf die die Kraft wirkt |
Ein Pascal (1 Pa) ist die Abkürzung für die Einheit ein Newton je Quadratmeter. Aus der Definitionsgleichung für den Druck ergibt sich:
Benannt ist die Einheit nach dem französischen Mathematiker und Physiker BLAISE PASCAL (1623-1662).
Druck kann in Flüssigkeiten und in Gasen auftreten. Auch feste Körper können auf andere Körper Druck ausüben.
Vielfache der Einheit 1 Pa sind ein Kilopascal (1 kPa) und ein Megapascal (1 MPa):
| 1 kPa = 1 000 Pa 1 MPa = 1 000 kPa = 1 000 000 Pa |
Da kleinere Flächen häufig in Quadratzentimetern angegeben sind, erhält man bei Rechnungen als Einheit oft . Als Umrechnung gilt hier:
Weitere, teils gesetzlich nicht mehr zugelassene oder nur in speziellen Bereichen verwendete Einheiten sind ein Bar (1 bar), eine Atmosphäre (1 at) oder ein Torr (1 Torr entspricht dem Druck von 1 mm Quecksilbersäule). Für diese Einheiten gilt:
| 1 bar = 100 000 Pa 1 at = 98 100 Pa 1 Torr = 133,32 Pa |
In der nachfolgenden Übersicht sind Werte für den Druck angegeben, die in Natur und Technik auftreten.
![]()
Der Druck in Flüssigkeiten und Gasen lässt sich gut mit dem Teilchenmodell deuten: In einer Flüssigkeit kommt der Druck durch die Kraftwirkung der Teilchen aufeinander und auf die Gefäßwände zustande.
In Gasen treffen die frei beweglichen Teilchen aufeinander und auf die Gefäßwände. Dabei über sie Kräfte auf Flächen aus, die sich als Druck bemerkbar machen.
-
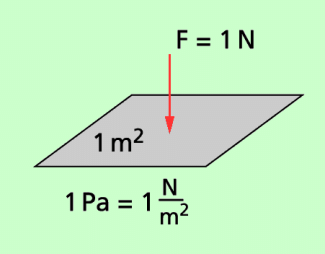
Die Einheit 1 Pascal
Berechnen des Druckes
Der auf eine Fläche wirkende Druck ist umso größer,
- je größer die auf die Fläche wirkende Kraft ist,
- je kleiner die Fläche ist.
Unter der Bedingung, dass die Kraft senkrecht auf die Fläche wirkt, kann der Druck p mit folgender Gleichung berechnet werden:
Die wirkende Kraft wird häufig als Druckkraft bezeichnet. Sie kann mit der Gleichung
berechnet werden, die man durch Umformung der Definitionsgleichung für den Druck erhält.
Messen des Druckes
Der Druck kann mithilfe von Druckmessers oder Manometern gemessen werden. Wichtige Bauformen sind das U-Rohr-Manometer und das Membran-Manometer. Genauere Hinweise sind unter dem Stichwort Manometer zu finden.
Druck in Flüssigkeiten und Gasen
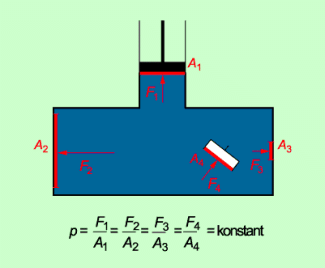
Der Druck in Flüssigkeiten, die sich in geschlossenen Gefäßen befinden, wird z. B. bei Bremsanlagen von Kraftfahrzeugen oder bei hydraulischen Pressen genutzt. Für den Druck in einer Flüssigkeit gilt die oben genannte allgemeine Definition für den Druck. Der Druck in einer Flüssigkeit, die sich in einem abgeschlossenen Gefäß befindet, ist überall näherungsweise gleich groß. Er breitet sich allseitig aus (Bild 3).
-
Druck in Flüssigkeiten
Der Druck in Gasen spielt z. B. bei Reifen, Bällen, Luftpumpen oder Gasflaschen eine wichtige Rolle. Für den Druck in einem Gas gilt ebenfalls die allgemeine Definition für den Druck. Der Druck in einem Gas, das sich in einem abgeschlossenen Gefäß befindet, ist überall näherungsweise gleich groß. Er breitet sich allseitig aus (Bild 4).
Der Druck fester Körper wird als Auflagedruck bezeichnet. Genauere Informationen dazu sind unter diesem Stichwort zu finden.
-
Druck in Gasen