Drehimpulserhaltungssatz

Analog zum Impulserhaltungssatz bei der Translation gilt für die Rotation ein Drehimpulserhaltungssatz. Er besagt, dass in einem abgeschlossenen System die Summe der Drehimpulse konstant ist, also gilt:

$\begin{array}{l} \vec{L} = \sum_{i = 1}^{n} {\vec{L}}_{i} = \sum_{i = 1}^{n} J_{i} \cdot {\vec{ω}}_{i} = konstant \\ \vec{L} Gesamtdrehimpuls \\ {\vec{L}}_{i} Drehimpulse der einzelnen Körper \\ J_{i} Trägheitsmomente der einzelnen Körper \\ {\vec{ω}}_{i} Winkelgeschwindigkeiten der einzelnen Körper \end{array}$

Dieser Drehimpulserhaltungssatz gilt in der Makrophysik einschließlich astronomischer Objekte ebenso wie im Bereich der Mikrophysik.

Drehmoment

#Winkelgeschwindigkeit #Drehmoment #Radius #Drehimpuls

Abgeschlossenes System bedeutet hierbei, dass auf das System keine äußeren Drehmomente wirken, die den Drehimpuls einzelner Körper des System beeinflussen würden.
Der Drehimpulserhaltungssatz gilt in der Makrophysik einschließlich astronomischer Objekte ebenso wie im Bereich der Mikrophysik.

Beispiele für Anwendungen

Gerade im Bereich des Sports findet man eine Reihe von Anwendungen des Drehimpulserhaltungssatzes.
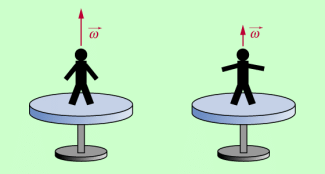
Bei vielen Sportarten (z.B. beim Eiskunstlaufen, beim Kunstspringen, beim Turnen, aber auch beim Fußball kommt es darauf an, schnelle Drehungen auszuführen, z.B. eine Pirouette zu drehen. Dabei wird genutzt, dass zwar der Drehimpuls, also das Produkt aus Trägheitsmoment und Winkelgeschwindigkeit, näherungsweise konstant ist, aber durch Änderung des Trägheitsmomentes sich auch die Winkelgeschwindigkeit ändert. Bild 2 zeigt den Zusammenhang, der dabei genutzt wird. Bei konstantem Drehimpuls bewirkt eine Verkleinerung des Trägheitsmomentes durch Anziehen von Armen und Beinen eine Vergrößerung der Winkelgeschwindigkeit. Umgekehrt bewirkt ein Ausstrecken von Armen und Beinen eine Vergrößerung des Trägheitsmomentes und damit eine Verkleinerung der Winkelgeschwindigkeit.
Experimentell kann man das leicht mithilfe eines Drehschemels demonstrieren (Bild 2).

Experimente mit einem Drehschemel: Die Winkelgeschwindigkeit kann in weiten Grenzen variiert werden.

Ein anderes Beispiel ist die Entstehung von Planetensystemen aus riesigen Gas- und Staubwolken (Bild 3). Hier wirkt neben dem Drehimpulserhaltungssatz das Gravitationsgesetz. Solche Gas- und Staubwolken besitzen eine bestimmte Rotationsenergie und damit einen bestimmten Drehimpuls. Verringern sich aufgrund der Gravitationswirkungen zwischen den Teilchen die Abmessungen der Wolke, so dreht sie sich aufgrund des Drehimpulserhaltungssatzes immer schneller um ihren Schwerpunkt. Die dadurch wirkende Fliehkraft hindert die Scheibenmaterie daran, in das Zentrum zu fallen. Vielmehr kommt es in der relativ stabilen Scheibe zu örtlichen Masseansammlungen, den Planetesimalen. Das sind die Keime der künftigen Asterioden und Planeten, an die sich weitere Materie anlagert und schließlich einen Himmelskörper bildet.
Auch unser Planetensystem ist vermutlich in dieser Weise entstanden. Für diese Theorie spricht auch, dass sich z.B. alle Planeten unseres Sonnensystems in gleichem Drehsinn und weitgehend in einer Ebene um die Sonne bewegen.

Drehimpuls und Rotationsenergie

Die Formel für die Rotationsenergie kann so umgeformt werden, dass die Beziehung zum Drehimpuls deutlich wird:

$\begin{array}{l} E_{rot} = \frac{1}{2} J \cdot ω^{2} = \frac{1}{2 J} J^{2} \cdot ω^{2} \\ Das Produkt J \cdot ω ist der Drehimpuls . Folglich \\ kann man auch schreiben: \\ E_{rot} = \frac{L^{2}}{2 J} \end{array}$

Auch hier wird die Analogie zur kinetischen Energie der Translation sichtbar. Dort gilt nämlich:

$\begin{array}{l} E_{kin} = \frac{1}{2} m \cdot v^{2} = \frac{1}{2 m} m^{2} \cdot v^{2} \\ Mit m \cdot v = p erhält man: \\ E_{kin} = \frac{p^{2}}{2 m} \end{array}$

Beide Gleichungen haben sich in der modernen Physik vielfach bewährt.

Gas- und Staubwolken besitzen einen bestimmten Drehimpuls. Er bleibt auch dann erhalten, wenn sich die Form der Gas- oder Staubwolke ändert.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel

Drehimpulserhaltungssatz

Drehmoment

Beispiele für Anwendungen

Drehimpuls und Rotationsenergie

Rechtliches

Einloggen