Kraftstoß und Impuls

Der Kraftstoß kennzeichnet die zeitliche Wirkung einer Kraft auf einen Körper. Der Impuls dagegen ist eine Größe, die den Bewegungszustand eines Körpers unter Einbeziehung seiner Masse charakterisiert. Zwischen diesen beiden Größen besteht ein enger Zusammenhang. Jeder Kraftstoß ist mit einer Impulsänderung verbunden:
$\vec{F} \cdot Δ t = m \cdot Δ \vec{v} oder \vec{I} = Δ \vec{p}$
Während der Kraftstoß einen Vorgang kennzeichnet und damit eine vektorielle Prozessgröße ist, beschreibt der Impuls den Bewegungszustand eines Körpers und ist eine vektorielle Zustandsgröße.

Die physikalische Größe Impuls

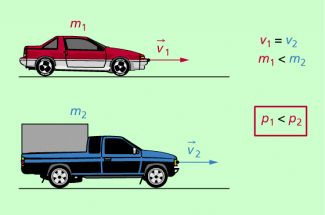
Den Bewegungszustand eines Körpers, z.B. einer Rakete (Bild 1), eines Autos, eines Balles oder eines Elektrons, kann man mit der physikalischen Größe Geschwindigkeit beschreiben. Will man diesen Bewegungszustand ändern, dann ist dazu eine bestimmte Kraft erforderlich, die von der Masse des Körpers abhängt. Auch bei der Einbeziehung möglicher Wirkungen, z.B. beim Stoß eines Körpers gegen eine Wand, spielen Geschwindigkeit und Masse des betreffenden Körpers eine Rolle.
Der Bewegungszustand eines Körpers wird dynamisch durch seine Masse und seine Geschwindigkeit gekennzeichnet. Zur Beschreibung nutzt man die physikalische Größe Impuls.

Eine Rakete, die sich mit einer bestimmten Geschwindigkeit bewegt, besitzt einen bestimmten Impuls, der von ihrer Geschwindigkeit und ihrer Masse abhängig ist.

Der Bewegungszustand eines Körpers bei der Translation wird durch den Impuls gekennzeichnet.

$\begin{array}{l} Formelzeichen: \vec{p} \\ Einheit: ein Kilogramm mal Meter durch Sekunde (1 kg \frac{m}{s} = 1 N \cdot s) \\ Er kann berechnet werden mit der Gleichung: \\ \vec{p} = m \cdot \vec{v} \\ m Masse des Körpers \\ \vec{v} Geschwindigkeit des Körpers \end{array}$

Der Impuls ist eine vektorielle (gerichtete) Größe, dessen Richtung mit der der Bewegungsrichtung des Körpers übereinstimmt. Er ist darüber hinaus eine Zustandsgröße, da er den Bewegungszustand eines Körpers charakterisiert. Diese Größe wurde deshalb früher auch als Bewegungsgröße bezeichnet.

Körper gleicher Geschwindigkeit und unterschiedlicher Masse besitzen einen unterschiedlichen Impuls.

Material zum Thema

Download

BWS-PHY2-0055-05

Format: MCD

Die physikalische Größe Kraftstoß

Um den Impuls eines Körpers zu ändern, gibt es unterschiedliche Möglichkeiten:

Es ändert sich die Masse des Körpers, bei einer Rakete z.B. durch Verbrennen und Ausstoßen von Treibstoff.
Es ändert sich der Betrag der Geschwindigkeit, z.B. durch Abbremsen des Körpers.
Es ändert sich die Richtung der Geschwindigkeit, z.B. bei einer Kurvenfahrt oder bei der Bewegung eines Satelliten um die Erde.

Betrag und Richtung der Geschwindigkeit eines Körpers können durch einwirkende Kräfte verändert werden (Bild 3). Die Wirkung einer Kraft auf einen Körper ist sowohl von Betrag und Richtung dieser Kraft als auch von der Zeitdauer ihrer Einwirkung abhängig. Das wird durch die physikalische Größe Kraftstoß erfasst.

Der Kraftstoß kennzeichnet die zeitliche Wirkung einer Kraft auf einen Körper.

$\begin{array}{l} Formelzeichen: \vec{I} \\ Einheit: ein Newton mal Sekunde (1 N \cdot s) \\ Unter der Bedingung, dass die Kraft im Zeitintervall konstant ist, \\ kann der Kraftstoß berechnet werden mit der Gleichung: \\ \vec{I} = \vec{F} \cdot Δ t \\ \vec{F} auf den Körper wirkende Kraft \\ Δ t Zeitdauer der Einwirkung \end{array}$

Der Kraftstoß ist eine vektorielle (gerichtete) Größe, dessen Richtung mit der der einwirkenden Kraft übereinstimmt. Er ist darüber hinaus eine Prozessgröße, da er den Vorgang der Bewegungsänderung eines Körpers charakterisiert.

Der Stoß oder Schlag gegen einen Ball ist ein Kraftstoß.

Zusammenhang zwischen Kraftstoß und Impuls

Jeder Kraftstoß ist mit einer Impulsänderung verbunden. Die quantitativen Zusammenhänge ergeben sich aus grundlegenden Gesetzen der Mechanik.
Wir betrachten dazu einen Körper der Masse m, auf den ein Kraftstoß mit einer konstanten Kraft ausgeübt wird:
$\begin{array}{l} \vec{F} \cdot Δ t \\ Setzt man für die Kraft \vec{F} = m \cdot \vec{a} (newtonsches Grundgesetz) \\ ein, so erhält man: \\ \vec{F} \cdot Δ t = m \cdot \vec{a} \cdot Δ t \\ Mit \vec{a} = \frac{Δ \vec{v}}{Δ t} ergibt sich: \\ \vec{F} \cdot Δ t = m \cdot \frac{Δ \vec{v}}{Δ t} \cdot Δ t oder \\ \vec{F} \cdot Δ t = m \cdot Δ \vec{v} \end{array}$

In Worten besagt die letzte Gleichung: Der Kraftstoß auf einen Körper ist gleich der Änderung seines Impulses.
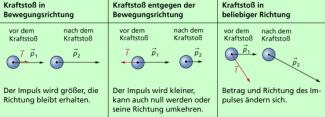
Drei charakteristische Fälle dieses Zusammenhangs sind in Bild 4 dargestellt.

Impuls und Kraft

Stellt man die zuletzt genannte Gleichung nach der Kraft um, dann erhält man:

$\vec{F} = \frac{m \cdot Δ \vec{v}}{Δ t} = \frac{Δ \vec{p}}{Δ t}$

Das ist eine Definition der Kraft, die inhaltlich bereits auf ISAAC NEWTON (1643-1727) zurückgeht. Sie ist allgemeiner als die Definition der Kraft mithilfe der Gleichung $F = m \cdot a$ , da in der Impulsänderung nicht nur der Fall der Geschwindigkeitsänderung, sondern auch der Fall der Änderung der Masse enthalten ist.

Zusammenhang zwischen Kraftstoß und Impuls für drei charakteristische Fälle.

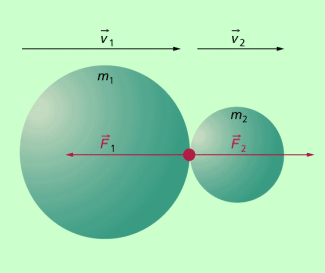
Die Stoßgleichung

Durch eine einfache Überlegung kann man auch einen quantitativen Zusammenhang für den Fall formulieren, dass zwei Körper zusammenstoßen (Bild 5). Ein Körper 1 $(Masse m_{1}, Geschwindigkeit {\vec{v}}_{1})$ stößt auf einen zweiten Körper $(Masse m_{2}, Geschwindigkeit {\vec{v}}_{2})$ . Beide Körper ändern als Folge des Stoßes ihre Geschwindigkeiten. Während des kurzen Zeitintervalls übt beim Zusammenstoß der Körper 1 auf den Körper 2 die Kraft aus und beschleunigt diesen (newtonsches Grundgesetz):
${\vec{F}}_{2} = m_{2} \cdot {\vec{a}}_{2} = m_{2} \cdot \frac{Δ {\vec{v}}_{2}}{Δ t}$

Nach dem Wechselwirkungsgesetz wirkt der Körper 2 mit der gleich großen aber entgegengesetzten Kraft zurück. Diese Überlegung führt unmittelbar auf die wichtige Stoßgleichung:
$\begin{array}{l} {\vec{F}}_{1} = - {\vec{F}}_{2} \\ m_{1} \cdot \frac{Δ {\vec{v}}_{1}}{Δ t} = - m_{2} \frac{Δ {\vec{v}}_{2}}{Δ t} \\ Multipliziert mit Δ t folgt: \\ m_{1} \cdot Δ {\vec{v}}_{1} = - m_{2} \cdot Δ {\vec{v}}_{2} \end{array}$

Drückt man diesen Zusammenhang mithilfe der Impulse aus, so kann man die Stoßgleichung auch folgendermaßen formulieren:
Die Änderung des Impulses von Körper 1 ist genauso groß wie die Änderung des Impulses von Körper 2, aber entgegengesetzt gerichtet.

$Δ {\vec{p}}_{1} = - Δ {\vec{p}}_{2}$

Dieser Zusammenhang spielt z.B. beim Zusammenstoß zweier Körper (Crash von Autos, zwei Billardkugeln, Tennisball - Tennisschläger) oder beim Rückstoß eine wichtige Rolle.