Impulserhaltungssatz

Für den Impuls gilt wie für die Energie und den Drehimpuls ein Erhaltungssatz, der als Impulserhaltungssatz oder als Gesetz von der Erhaltung des Impulses bezeichnet wird. Er lautet:

In einem kräftemäßig abgeschlossenen System bleibt der Gesamtimpuls erhalten. Es gilt:
$\vec{p} = \sum_{i = 1}^{n} {\vec{p}}_{i} = \sum_{i = 1}^{n} m_{i} \cdot {\vec{v}}_{i} = konstant$

Drehmoment

#Winkelgeschwindigkeit #Drehmoment #Radius #Drehimpuls

Der Impulserhaltungssatz ist ein grundlegender Erfahrungssatz, der sowohl in der Makrophysik als auch in der Mikrophysik gilt.

Kräftemäßig abgeschlossen bedeutet, dass keine äußere Kraft auf das System einwirkt, die seinen Gesamtimpuls verändern würde. Dagegen können innere Kräfte , also Kräfte innerhalb des Systems, in beliebiger Weise wirken. Der Impulserhaltungssatz ist ein grundlegender Erfahrungssatz, der sowohl in der Makrophysik als auch in der Mikrophysik gilt.

Impulserhaltungssatz für zwei wechselwirkende Körper

Besonders häufig tritt der Fall auf, dass an einer Wechselwirkung zwei Körper beteiligt sind. Dabei ist es oft erforderlich, den Impuls der Körper vor und nach der Wechselwirkung zu berechnen.
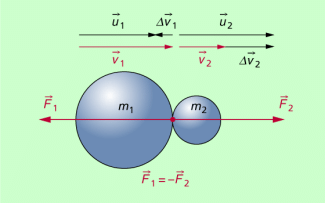
Als Beispiel betrachten wir zwei Kugeln unterschiedlicher Massen und Geschwindigkeiten, die zusammenstoßen.
Durch den Vergleich der Situation vor und nach dem Stoß mithilfe der Stoßgleichung
$m_{1} \cdot Δ {\vec{v}}_{1} = - m_{2} \cdot Δ {\vec{v}}_{2}$
erhält man eine Gleichung, die eine der wichtigsten Konsequenzen aus den newtonschen Gesetzen darstellt: einen Erhaltungssatz. Ein Erhaltungssatz beschreibt eine Beziehung zwischen physikalischen Größen, die während des Ablaufes der Bewegung oder eines anderen Prozesses invariant ist.

$\begin{array}{l} Dazu führen wir mit {\vec{u}}_{1} und {\vec{u}}_{2} die jeweiligen \\ Geschwindigkeiten nach dem Stoß ein . \\ {\vec{v}}_{1} und {\vec{v}}_{2} sind die Geschwindigkeiten \\ vor dem Stoß: \\ Δ {\vec{v}}_{1} = {\vec{u}}_{1} - {\vec{v}}_{1} und Δ {\vec{v}}_{2} = {\vec{u}}_{2} - {\vec{v}}_{2} \\ Aus m_{1} \cdot Δ {\vec{v}}_{1} = - m_{2} \cdot Δ {\vec{v}}_{2} folgt damit: \\ m_{1} Δ {\vec{v}}_{1} = - m_{2} \cdot Δ {\vec{v}}_{2} \\ m_{1} ({\vec{u}}_{1} - {\vec{v}}_{1}) = - m_{2} ({\vec{u}}_{2} - {\vec{v}}_{2}) \\ m_{1} {\vec{u}}_{1} - m_{1} \cdot {\vec{v}}_{1} = - m_{2} \cdot {\vec{u}}_{2} + m_{2} {\vec{v}}_{2} \end{array}$

Ordnet man die Größen in der Gleichung so um, dass alle Größen, die die Körper vor dem Stoß beschreiben, auf der linken Seite stehen und rechts sämtliche Größen nach dem Stoß, so erhält man:

$m_{1} \cdot {\vec{v}}_{1} + m_{2} \cdot {\vec{v}}_{2} = m_{1} \cdot {\vec{u}}_{1} + m_{2} \cdot {\vec{u}}_{2}$

Das heißt in Worten: Die Summe der Impulse vor dem Stoß (linke Seite) ist gleich der Summe der Impulse nach dem Stoß (rechte Seite).

Der Schwerpunktsatz

Man kann den genannten Zusammenhang auf sämtliche Körper eines Systems anwenden, das abgeschlossen ist (abgeschlossenes System), in dem also alle actio- und reactio-Kräfte vollständig berücksichtigt sind und nur innere Kräfte wirken. Die Kräfte, die von außen auf das System einwirken (äußere Kräfte), werden nicht berücksichtigt. Als Verallgemeinerung erhält man den überaus wichtigen Schwerpunktsatz .
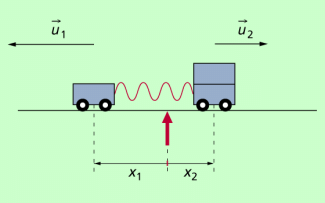
Zu Beginn des Experimentes nach Bild 3 hält ein dünner Faden die beiden Wagen gegen die gespannte Feder zusammen. Die Wagen sind in Ruhe, der Gesamtimpuls ist null:

${\vec{p}}_{g e s} = 0$

Reißt der Faden, streben die zwei Wagen mit unterschiedlichen Geschwindigkeiten auseinander, der leichtere Wagen schneller als der schwerere. Jeder Wagen für sich bekommt einen Impuls. Die Vektorsumme dieser Impulse muss aber wieder null sein, da keine äußeren Kräfte gewirkt haben. Das System war kräftemäßig abgeschlossen. Demzufolge gilt:

$\begin{array}{l} {\vec{p}}_{g e s} = m_{1} \cdot {\vec{u}}_{1} + m_{2} \cdot {\vec{u}}_{2} = 0 \\ oder \\ m_{1} \cdot {\vec{u}}_{1} = - m_{2} \cdot {\vec{u}}_{2} \end{array}$

Das Minuszeichen zeigt an, dass die Geschwindigkeiten entgegengesetzt sind. Sind die Massen gleich, sind es auch die Beträge der Geschwindigkeiten. Sind die Massen nicht gleich, verhalten sich die Geschwindigkeitsbeträge umgekehrt wie die Massen:

$\frac{u_{1}}{u_{2}} = \frac{m_{2}}{m_{1}}$

War das System vor dem Durchbrennen des Fadens im Gleichgewicht, unterstützte also die rote Spitze das System im Schwerpunkt, so ändert sich daran auch nichts, wenn der Faden durchbrennt und die Wagen auseinanderfahren. Denn im Falle des Gleichgewichts gilt „vor der Explosion“, bevor also die beiden Wagen auseinanderstreben:
$m_{1} \cdot x_{1} = m_{2} \cdot x_{2}$

Dies gilt wegen des Impulserhaltungsatzes auch nach dem Durchbrennen des Fadens für die Positionen $x_{1} (t) und x_{2} (t)$ der Wagen zu jedem Zeitpunkt t:

$x_{1} (t) = x_{1} + u_{1} und x_{2} (t) = x_{2} + u_{2}$

Das Verhältnis der beiden Abstände vom Drehpunkt hat nämlich zu jedem Zeitpunkt den Wert, der einer Unterstützung in Schwerpunktslage entspricht:

$\begin{array}{l} \frac{x_{1} (t)}{x_{2} (t)} = \frac{x_{1} + u_{1}}{x_{2} + u_{2}} = \frac{x_{1} + u_{1}}{x_{1} \frac{m_{1}}{m_{2}} + u_{1} \frac{m_{1}}{m_{2}}} \\ \frac{x_{1} (t)}{x_{2} (t)} = \frac{m_{2}}{m_{1}} \end{array}$

Mit anderen Worten: Der Schwerpunkt hat sich nicht verschoben. Er wird durch innere Kräfte nicht beeinflusst (Bild 4). Dieser Sachverhalt wird als Schwerpunktsatz bezeichnet und kann zusammenfassend folgendermaßen formuliert werden:

Der Schwerpunkt eines abgeschlossenen Systems wird durch innere Kräfte nicht verschoben.

Damit verändert sich z.B. auch nicht der Schwerpunkt eines explodierenden Feuerwerkskörpers, da bei der Explosion nur innere Kräfte wirken. Der Schwerpunktsatz gilt auch für das berühmte Beispiel des Barons von MÜNCHHAUSEN, der sich angeblich am eigenen Schopf aus dem Sumpf gezogen hat. Da in diesem Falle nur innere Kräfte wirken, kann der Schwerpunkt des Systems nicht verschoben werden. Mit anderen Worten: Die Geschichte des Lügenbarons ist physikalisch nicht möglich.

Lernprobleme in Physik?

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

KI-Tutor Kim hilft bei allen schulischen Problemen
Individuelle, kindgerechte Förderung in Dialogform
Lernplattform für 9 Fächer ab der 4. Klasse
Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
Rund um die Uhr für dich da

Jetzt in Physik durchstarten

Verwandte Artikel

Angaben zum Lexikon

Impressum

Impulserhaltungssatz

Drehmoment

Impulserhaltungssatz für zwei wechselwirkende Körper

Der Schwerpunktsatz

Rechtliches

Einloggen