Einteilung von Stößen

Stöße treten in Natur, Technik und Alltag in vielfältiger Art auf. Nach der Energiebilanz unterscheidet man zwischen unelastischen und elastischen Stößen. Nach der Lage der Körper, die sie beim Stoß zueinander haben, differenziert man zwischen geraden und schiefen Stößen. Darüber hinaus kann ein Stoß zentral oder nicht zentral sein. Alle genannten Arten von Stößen sind Idealisierungen, die in der Praxis nur näherungsweise auftreten.

Beispiele für Stöße sind der Schlag eines Tennisschlägers gegen einen Tennisball (Bild 1), der Treffer eines Boxers, das Halten eines Balles durch einen Torwart, das Auftreffen eines Geschosses auf einen Körper, ein Hammerschlag auf einen Nagel oder der Zusammenstoß zweier Elementarteilchen.

Nach der Energiebilanz unterscheidet man zwischen unelastischen und elastischen Stößen. Nach der Lage der Körper, die sie beim Stoß zueinander haben, differenziert man zwischen geraden und schiefen Stößen. Darüber hinaus kann ein Stoß zentral oder nicht zentral sein. Alle genannten Arten von Stößen sind Idealisierungen, die in der Praxis nur näherungsweise auftreten. Deshalb muss man bei einem gegebenen Beispiel prüfen, was für eine Art von Stoß im betreffenden Fall näherungsweise vorliegt und welche Gesetze demzufolge angewendet werden können.

Ein Schlag eines Tennisschlägers gegen einen Tennisball ist näherungsweise ein zentraler elastischer Stoß.

Einteilung von Stößen - zentraler elastischer Stoß

MEV Verlag, Augsburg

Unelastische und elastische Stöße

Nach der Energiebilanz unterscheidet man zwischen unelastischen, teilelastischen und elastischen Stößen. Betrachtet wird dabei in der Regel nur die kinetische Energie der Stoßpartner. Es wird also davon ausgegangen, dass die Bewegungen nur in einer Ebene erfolgen (potenzielle Energie ändert sich nicht) und keine Rotation auftritt.

Unelastischer Stoß: Ein unelastischer Stoß liegt vor, wenn bei der Wechselwirkung der Körper nur unelastische Verformungen auftreten, sich die Körper also nach dem Stoß mit einer gemeinsamen Geschwindigkeit weiterbewegen. Man spricht auch von einem ideal unelastischen Stoß. Beim Stoß wird ein Teil der kinetischen Energie oder die gesamte kinetische Energie in andere Energieformen umgewandelt. Der letzte Fall würde auftreten, wenn sich zwei Körper gleicher Masse und gleicher Geschwindigkeit aufeinander zu bewegen und zusammenstoßen oder wenn der Stoß gegen eine feste Wand erfolgt.
Für den Impuls der beteiligten Körper vor und nach dem Stoß gilt der Impulserhaltungssatz in der Form:

$m_{1} \cdot {\vec{v}}_{1} + m_{2} \cdot {\vec{v}}_{2} = (m_{1} + m_{2}) \cdot \vec{u}$

Für die Verringerung der kinetischen Energie gilt:

$Δ E_{kin} = \frac{1}{2} m_{1} \cdot v_{1}^{2} + \frac{1}{2} m_{2} \cdot v_{2}^{2} - \frac{1}{2} (m_{1} + m_{2}) u^{2}$

Ausführliche Hinweise sind unter dem Stichwort „Zentraler unelastischer Stoß“ zu finden.

Teilelastischer Stoß: Ein teilelastischer Stoß liegt vor, wenn die Wechselwirkung der Körper teils unelastisch und teils elastisch erfolgt. Dabei wird ein Teil der kinetischen Energie der Stoßpartner in andere Energieformen umgewandelt. Das ist der Fall, der in der Praxis am häufigsten auftritt, zugleich aber mathematisch am schwersten zu beschreiben ist, weil man z.B. für Energiebilanzen wissen muss, wie groß der Anteil der unelastischen Wechselwirkungen ist. Erfasst werden kann das durch den Stoßfaktor k, für den gilt:

unelastischer Stoß	k = 0
teilelastischer Stoß	0 > k > 1
elastischer Stoß	k = 1

Dieser Stoßfaktor geht als Faktor in die Energiebilanz ein, sodass z.B. für die Geschwindigkeiten der Körper nach einem teilelastischen Stoß gilt:

$\begin{array}{l} u_{1} = \frac{m_{1} \cdot v_{1} + m_{2} \cdot v_{2} - m_{2} (v_{1} - v_{2}) k}{m_{1} + m_{2}} \\ u_{2} = \frac{m_{1} \cdot v_{1} + m_{2} \cdot v_{2} - m_{1} (v_{2} - v_{1}) k}{m_{1} + m_{2}} \end{array}$

Elastischer Stoß: Ein elastischer Stoß, auch ideal elastischer Stoß genannt liegt vor, wenn nur elastische Verformungen auftreten und damit die kinetische Energie der Stoßpartner vor dem Stoß genauso groß ist wie nach dem Stoß.
Für den Impuls der beteiligten Körper vor und nach dem Stoß gilt der Impulserhaltungssatz in der Form:

$m_{1} \cdot {\vec{v}}_{1} + m_{2} \cdot {\vec{v}}_{2} = m_{1} \cdot {\vec{u}}_{1} + m_{2} \cdot {\vec{u}}_{2}$

Für die kinetische Energie gilt:

$\begin{array}{l} E_{kin,vor} = E_{kin,nach} \\ \frac{1}{2} m_{1} \cdot v_{1}^{2} + \frac{1}{2} m_{2} \cdot v_{2}^{2} = \frac{1}{2} m_{1} \cdot u_{1}^{2} + \frac{1}{2} m_{2} \cdot u_{2}^{2} \end{array}$

Ausführliche Hinweise sind unter dem Stichwort „Zentraler elastischer Stoß“ zu finden.

Gerade und schiefe Stöße

Unterscheiden kann man Stöße auch nach der Lage der Körper, die sie vor dem Zusammenstoß zueinander haben.
Ein gerader Stoß liegt vor, wenn die Richtungen der Geschwindigkeiten bzw. der Impulse der Körper auf einer Linie liegen, die durch die Schwerpunkte der beiden Körper verläuft.
Ein schiefer Stoß liegt vor, wenn die Geschwindigkeiten bzw. Impulse nicht auf einer Linie liegen, die durch die Schwerpunkte der Körper verläuft.

Zentrale und nicht zentrale Stöße

Nach der Lage der Körper bei der Wechselwirkung unterscheidet man zwischen zentralen und nicht zentralen Stößen.
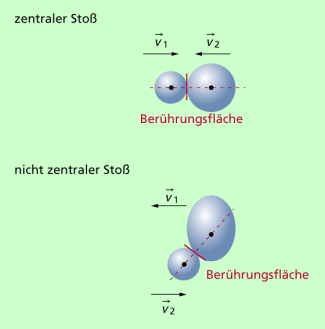
Ein zentraler Stoß liegt vor, wenn die Verbindungsgerade der Schwerpunkte beider Körper senkrecht auf der Berührungsfläche steht, die sich beim Stoß ausbildet (Bild 4). Stoßen Kugeln zusammen, so ist diese Bedingung immer erfüllt. Ein Stoß von Kugeln ist damit immer ein zentraler Stoß.
Ein nicht zentraler Stoß liegt vor, wenn die oben genannte Bedingung nicht erfüllt ist (Bild 4).

Zentrale und nicht zentrale Stöße

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel

Einteilung von Stößen

Unelastische und elastische Stöße

Gerade und schiefe Stöße

Zentrale und nicht zentrale Stöße

Rechtliches

Einloggen