Drehimpuls

Bei der Translation charakterisiert der Impuls den Bewegungszustand eines Körpers. In analoger Weise lässt sich bei der Rotation der Bewegungszustand eines rotierenden starren Körpers durch die physikalische Größe Drehimpuls kennzeichnen. Der Drehimpuls eines Körpers kann berechnet werden mit der Gleichung:

$\begin{array}{l} \vec{L} = J \cdot \vec{ω} \\ J Trägheitsmoment des Körpers \\ \vec{ω} Winkelgschwindigkeit \end{array}$

Drehmoment

#Winkelgeschwindigkeit #Drehmoment #Radius #Drehimpuls

Kreisbewegung

#Winkelgeschwindigkeit #Drehmoment #Radius #Drehimpuls

Definition des Drehimpulses

Bei der Translation charakterisiert der Impuls den Bewegungszustand eines Körpers. In analoger Weise lässt sich bei der Rotation der Bewegungszustand eines rotierenden starren Körpers durch die physikalische Größe Drehimpuls kennzeichnen. Der Bewegungszustand eines rotierenden starren Körpers wird durch seine Winkelgeschwindigkeit und sein Trägheitsmoment bestimmt. Allgemein gilt:

Der Bewegungszustand eines rotierenden starren Körpers wird durch den Drehimpuls gekennzeichnet.

Formelzeichen: $\vec{L}$
Einheit: ein Kilogramm mal Quadratmeter durch Sekunde $(1 \frac{kg \cdot m^{2}}{s})$

Der Drehimpuls eines Körpers kann berechnet werden mit der Gleichung:

$\begin{array}{l} \vec{L} = J \cdot \vec{ω} \\ J Trägheitsmoment des Körpers \\ \vec{ω} Winkelgschwindigkeit \end{array}$

Formal erhält man die genannte Gleichung, wenn man vom Impuls ausgeht und dort die analogen Größen der Drehbewegung einsetzt: Die Masse beim Impuls wird ersetzt durch das Trägheitsmoment beim Drehimpuls. Die Geschwindigkeit wird ersetzt durch die analoge Größe Winkelgeschwindigkeit.
Rotieren mehrere Teilchen mit den Massen $m_{i}$ und dem jeweiligen Drehimpuls ${\vec{L}}_{i} = m_{i} \cdot r_{i}^{2} \cdot \vec{ω}$ , dann ist der gesamte Drehimpuls:

$\begin{array}{l} \vec{L} = \sum_{i = 1}^{n} {\vec{L}}_{i} = \sum_{i = 1}^{n} m_{i} \cdot r_{i}^{2} \cdot {\vec{ω}}_{i} \\ Nimmt man an, dass alle Teilchen mit der gleichen \\ Winkelgeschwindigkeit rotieren, so ergibt sich: \\ \vec{L} = \vec{ω} \cdot \sum_{i = 1}^{n} m_{i} \cdot r_{i}^{2} \\ Der rechts stehende Ausdruck ist das Trägheitsmoment . \\ Somit ergibt sich: \\ \vec{L} = \vec{ω} \cdot J \end{array}$

Der Drehimpuls spielt nicht nur bei Körpern, sondern in der Quantenphysik auch bei Elementarteilchen eine Rolle. Er wird dort als Spin bezeichnet.

Der Drehimpuls als vektorielle Zustandsgröße

Wie der Impuls ist auch der Drehimpuls eine vektorielle Größe. Da die Winkelgeschwindigkeit ein axialer Vektor ist, gilt das auch für den Drehimpuls. Ermittelt werden kann die Richtung mithilfe der rechten Hand: Wenn die gekrümmten Finger in Drehrichtung zeigen, dann gibt der Daumen die Richtung der Winkelgeschwindigkeit und des Drehimpulses an.
Darüber hinaus kennzeichnet der Drehimpuls den Zustand eines Körpers. Er ist somit eine vektorielle Zustandsgröße.

Drehimpuls und Drehmoment

Bei der Translation besteht zwischen Impuls und Kraft ein enger Zusammenhang: Wirkt auf einen Körper eine bestimmte Zeit lang eine Kraft, so ändert sich sein Impuls. Man kann auch formulieren: Die Kraft ist gleich der zeitlichen Änderung des Impulses:

$\vec{F} = \frac{Δ \vec{p}}{Δ t}$
Analoge Überlegungen kann man auch für den Drehimpuls und die Größe Drehmoment vornehmen: Wirkt auf einen drehbar gelagerten Körper ein Drehmoment, so ändert sich sein Drehimpuls. Das Drehmoment ist gleich der zeitlichen Änderung des Drehimpulses:

$\vec{M} = \frac{Δ \vec{L}}{Δ t}$

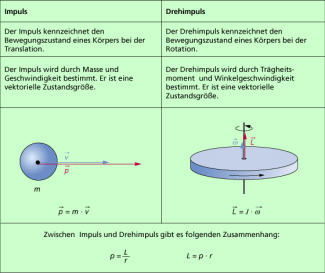
Vergleich von Impuls und Drehimpuls
In Bild 4 sind Impuls und Drehimpuls in einer Übersicht gegenübergestellt.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel