Größen zur Beschreibung der Rotation

Die translatorische Bewegung eines Körpers kann mit den Größen Weg, Geschwindigkeit und Beschleunigung beschrieben werden. Analog dazu kann man die Bewegung eines rotierenden starren Körpers mit den Größen Drehwinkel, Winkelgeschwindigkeit und Winkelbeschleunigung beschreiben. Teilweise werden auch die Größen Umlaufzeit und Drehzahl mit genutzt. In der Dynamik kommen als weitere Größen das Drehmoment und das Trägheitsmoment hinzu.

Drehzahl und Umlaufzeit

Eine Möglichkeit zur Beschreibung rotierender Körper besteht darin, ihre Drehzahl und ihre Umlaufzeit anzugeben. So führt z.B. der Sekundenzeiger einer Uhr in einer Minute eine vollständige Umdrehung aus. Seine Drehzahl beträgt dann 1/min. Ein Punkt auf der Erdoberfläche rotiert in 24 Stunden einmal um die Erdachse. Seine Drehzahl hat einen Wert von 1/(24 Stunden).
Allgemein gilt:

Die Drehzahl gibt an, wie viele Umdrehungen um eine Achse ein Körper in einer bestimmten Zeiteinheit ausführt.
Formelzeichen: n
Einheit: eins durch Sekunde $(\frac{1}{s} = s^{- 1})$
Die Zeit für einen vollen Umlauf wird als Umlaufzeit bezeichnet.
Formelzeichen: T
Einheit: eine Sekunde (1 s)

Zwischen den beiden Größen Drehzahl und Umlaufzeit besteht ein einfacher Zusammenhang:

$T = \frac{1}{n} oder n = \frac{1}{T}$

Beträgt in einer beliebigen Zeit t die Anzahl der Umdrehungen N, so gelten für die Umlaufzeit T bzw. die Drehzahl n die folgenden Beziehungen:

$T = \frac{N}{t} n = \frac{t}{N}$

Drehwinkel und Weg

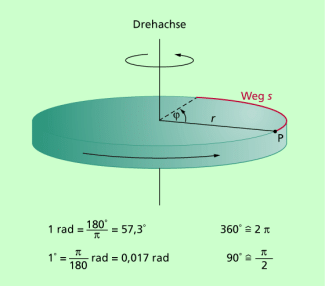
Als Maß für die Drehung eines starren Körpers wird der Drehwinkel gewählt (Bild 2).

Der Drehwinkel gibt an, um welchen Winkel ein Körper gedreht wird.

Formelzeichen: $ϕ$
Einheit: ein Grad (1°) oder ein Radiant (1 rad)

Eine volle Umdrehung entspricht einem Winkel von 360° in Gradmaß oder $2 π$ in Bogenmaß. Damit gilt:

$1 rad = \frac{180 °}{π} = 57,3 ° 1° = \frac{π}{180 °} rad = 0,017 rad$

Häufig wird die Einheit rad weggelassen. Als einfache Beziehungen zwischen Gradmaß und Bogenmaß kann man sich merken:

$\begin{array}{l} 360 ° = 2 π \\ 180 ° = π \\ 90 ° = \frac{π}{2} \end{array}$

Zwischen dem Drehwinkel und dem Weg, den ein Punkt P zurücklegt (Bild 2), gilt die Beziehung:

$\begin{array}{l} s = ϕ \cdot r \\ s vom Punkt P zurückgelegter Weg \\ ϕ Drehwinkel \\ r Abstand des Punktes P von der Drehachse \end{array}$

Winkelgeschwindigkeit und Bahngeschwindigkeit

Die Schnelligkeit der Änderung des Drehwinkels wird durch die physikalische Größe Winkelgeschwindigkeit erfasst.

Die Winkelgeschwindigkeit gibt an, wie schnell sich der Drehwinkel ändert.

$\begin{array}{l} Formelzeichen: ω \\ Einheit: eins durch Sekunde (\frac{1}{s} = s^{- 1}) \end{array}$

Die Winkelgeschwindigkeit kann berechnet werden mit der Gleichung:
$ω = \frac{Δ ϕ}{Δ t}$
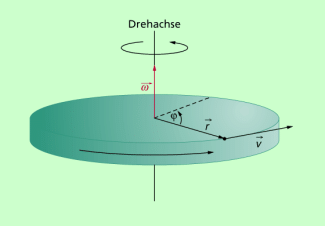
Die Winkelgeschwindigkeit ist eine vektorielle Größe. Ihre Richtung zeigt immer in Richtung der Drehachse und ergibt sich mithilfe der Rechte-Hand-Regel (Korkenzieherregel): Zeigen die gekrümmten Finger der rechten Hand in Drehrichtung des Körpers, so gibt die Richtung des Daumens die Richtung der Winkelgeschwindigkeit an. Mathematisch ist die Winkelgeschwindigkeit das Vektorprodukt (Kreuzprodukt) aus dem Radius und der Geschwindigkeit:
$\vec{ω} = \vec{r} \times \vec{v}$
Die Winkelgeschwindigkeit kann auch aus der Drehzahl und der Umlaufzeit ermittelt werden, denn für den Zusammenhang zwischen diesen Größen gilt:
$ω = \frac{2 π}{T} = 2 π \cdot n$

Ein Punkt P eines rotierenden starren Körpers weiter weg von der Drehachse legt bei gleichem Drehwinkel je Zeiteinheit und damit bei gleicher Winkelgeschwindigkeit einen größeren Kreisbogen und damit auch einen größeren Weg zurück als ein Punkt nahe an der Drehachse. Die Geschwindigkeit, mit der sich ein Punkt eines starren Körpers auf einer Kreisbahn bewegt, wird als Bahngeschwindigkeit bezeichnet. Zwischen der Winkelgeschwindigkeit des starren Körpers und der Bahngeschwindigkeit eines seiner Punkte besteht die folgende Beziehung:

$\begin{array}{l} v = ω \cdot r \\ v Bahngeschwindigkeit eines Punktes \\ ω Winkelgeschwindigkeit des Körpers \\ r Abstand des Punktes von der Drehachse \end{array}$

Bei einer gleichförmigen Rotation ist die Winkelgeschwindigkeit konstant, bei einer beschleunigten Rotation (Anlaufen einer Motorwelle) oder einer verzögerten Rotation (Abbremsen eines Schwungrades) verändert sie sich mit der Zeit.

Winkelbeschleunigung und Bahnbeschleunigung

Die Schnelligkeit der Änderung der Winkelgeschwindigkeit wird durch die physikalische Größe Winkelbeschleunigung erfasst.

Die Winkelbeschleunigung gibt an, wie schnell sich die
Winkelgeschwindigkeit eines rotierenden Körpers ändert.

$\begin{array}{l} Formelzeichen: α \\ Einheit: eins durch Quadratsekunde (\frac{1}{s^{2}} = s^{- 2}) \end{array}$

Die Winkelbeschleunigung kann berechnet werden mit der Gleichung:
$α = \frac{Δ ω}{Δ t}$

Sie ist wie die Winkelgeschwindigkeit eine vektorielle Größe. Ihre Richtung stimmt mit der der Winkelgeschwindigkeit überein. Die Winkelbeschleunigung ist somit auch ein axialer Vektor.

Rotiert ein Körper beschleunigt, so bewegen sich auch seine einzelnen Punkte längs ihrer Bahn beschleunigt. Diese Beschleunigung eines Punktes auf seiner Bahn wird als Bahnbeschleunigung bezeichnet. Zwischen der Winkelbeschleunigung und der Bahnbeschleunigung gilt folgende Beziehung:
$\begin{array}{l} a = α \cdot r \\ a Bahnbeschleunigung eines Punktes \\ α Winkelbeschleunigung des Körpers \\ r Abstand des Punktes von der Drehachse \end{array}$

Weitere Größen und Zusammenhänge

Mit den genannten Größen können alle kinematischen Zusammenhänge bei der Rotation beschrieben werden. Bezieht man die Dynamik mit ein, so sind weitere Größen erforderlich. Es handelt sich dabei um das Drehmoment und das Trägheitsmoment. Genauere Informationen sind unter diesen Stichwörtern zu finden.

Ein Vergleich der oben genannten Gleichungen zeigt, dass zwischen den Größen der Translation und den entsprechenden Größen der Rotation ein jeweils völlig analoger Zusammenhang besteht. Für die kinematischen Größen ist dieser Zusammenhang in Bild 4 dargestellt.