Relativität der Masse
Die Masse in der Relativitätstheorie
Die Masse wird in der modernen Physik wie in der klassischen Physik meist als eine Konstante angesehen, die unabhängig vom Beobachter ist (Lorentzinvariante). Um allerdings weiterhin die Formeln aus der klassischen Mechanik verwenden zu können, kann eine relativistische Masse eingeführt werden, die sich von der sogenannten Ruhemasse unterscheidet.
Die Ruhemasse ist die Masse eines Körpers oder Teilchens, die ein Beobachter registriert, der sich in einem Intertialsystem gegenüber dem Körper oder dem Teilchen in Ruhe befindet.
Die relativistische Masse (seltener dynamische Masse oder Impulsmasse genannt) ist die Masse eines Körpers oder Teilchens, die ein Beobachter registriert, der sich in einem Inertialsystem gegenüber dem Körper oder dem Teilchen mit relativistischer Geschwindigkeit bewegt.
Wichtig ist, dass sich die innere Struktur eines Körpers dabei nicht ändert. Es kommen keine Atome oder Ähnliches hinzu. Lediglich seine Trägheit und Schwere werden größer (vgl. träge und schwere Masse).
Dabei ist:
- die relativistische Masse
- die Ruhemasse
- die Geschwindigkeit des Teilchens im Inertialsystem
- die Lichtgeschwindigkeit
- k der LORENTZ-Faktor
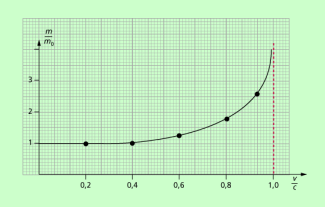
Auf die Ruhemasse normiert, ergibt sich folgender graphischer Zusammenhang zwischen und
Aktuelle Sicht auf die Relativität der Masse
Die Masse relativistisch zu betrachten ist eine hilfreiche Sichtweise bei verschiedenen Problemen. Beispielsweise können experimentelle Befunde auf diese Weise einfach erklärt werden. Vermehrt verzichten Physiker heutzutage allerdings auf diese Interpretation. Sie nehmen die Masse als konstant an. Stattdessen wird der Impuls grundsätzlich in einer relativistischen Form definiert:
Bei Körpern, die sich mit relativistischen Geschwindigkeiten bewegen, kann trotzdem eine Zunahme der Trägheit und der Gravitation beobachtet werden. Diese Zunahme hat ihren Ursprung allerdings nicht in den Körpern selbst, sondern in den Eigenschaften der Raumzeit.
Alle folgenden Abschnitte sind also als Beispiele zu verstehen, wie weit die Interpretation der Relativität der Masse die Physik trägt. Diese Interpretaion ist aber nicht notwendig.
Experimentelle Befunde
Mithilfe der trägen Masse kann z. B. die Trägheitszunahme von Teilchen bei relativistischen Geschwindigkeiten erklärt werden. Elektronen können vergleichsweise einfach durch entsprechende Beschleunigungsspannungen auf solche Geschwindigkeiten gebracht werden.
Der experimentelle Nachweis der scheinbaren Vergrößerung der Masse mit der Geschwindigkeit wurde erstmals 1909/10 durch die Physiker KAUFMANN und BUCHERER bei Elektronen nachgewiesen. Die folgende Übersicht zeigt den Zusammenhang zwischen Geschwindigkeit und Masse für Elektronen. Auch die erforderliche Beschleunigungsspannung ist angegeben, um die Elektronen aus der Ruhe auf die jeweilige Geschwindigkeit zu bringen.
Beschleunigungs-spannung in Volt | Geschwindigkeit der Elektronen in | Elektronenmasse im Verhältnis zu Ruhemasse |
|---|---|---|
| 0 | 0 | 1 |
| 1 000 | 18 700 | 1,001 9 |
| 10 000 | 58 700 | 1,019 3 |
| 100 000 | 164 800 | 1,262 |
| 1 000 000 | 283 000 | 2,87 |
| 10 000 000 | 299 210 | 13,8 |
Herleitung der Gleichung für die relativistische Masse
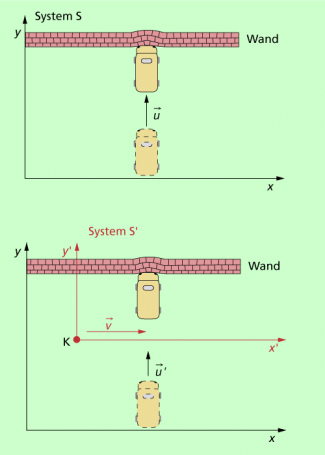
Die Gleichung für die relativistische Masse lässt sich ausgehend von einem Gedankenexperiment herleiten, bei dem die Impulse aus der Sicht verschiedener Inertialsysteme verglichen werden. Dazu betrachten wir einen Körper, der vollkommen unelastisch gegen eine Wand stößt, aus der Sicht zweier Bezugssysteme und (siehe Abbildung).
Aus der Sicht des mit der Mauer verbundenen ruhenden Systems stößt das Auto unelastisch gegen die Wand und hinterlässt eine bestimmte Wirkung. Ursache dafür ist sein Impuls .
Aus der Sicht des Systems , das sich mit hoher Geschwindigkeit in x-Richtung bewegt, tritt die gleiche Wirkung auf, die nur durch einen gleich großen Impuls hervorgerufen sein kann. Wegen der Zeitdilatation muss aber der Vorgang für einen Beobachter in viel langsamer verlaufen. Die gleiche Wirkung ist nur dann erklärlich, wenn von aus die Masse des Körpers sehr viel größer ist.
Da offensichtlich die Wirkungen und damit die Impulse unabhängig vom gewählten System sind, kann man setzen:
Setzt man die Gleichungen (2) und (3) unter Einbeziehung von Gleichung (4) in die Gleichung (1) ein, so erhält man:
Mit der Masse m als Ruhemasse und der Masse m' als relativistischer Masse erhält man die weiter oben genannte Gleichung.
Folgerungen aus der Veränderlichkeit der Masse
Bei den im Alltag üblichen Geschwindigkeiten ist die Massezunahme mit der Geschwindigkeit vernachlässigbar klein und braucht nicht beachtet zu werden. Mit dem Konzept der relativistischen Masse können aber verschiedene relativistische Phänomene anschaulich erklärt werden:
- Wirkt auf einen Körper oder auf ein Teilchen eine konstante Kraft, so ist die Beschleunigung wegen der mit der Geschwindigkeit wachsenden Masse nicht mehr konstant, sondern nimmt ab.
- Da die Masse mit Annäherung an die Lichtgeschwindigkeit stark zunimmt, ist für eine bestimmte Beschleunigung eine immer größere Kraft erforderlich. Das ist z. B. die Erklärung für die Notwendigkeit sehr starker Magnete in Beschleunigern.
- Bei Lichtgeschwindigkeit wäre die Masse eines Körpers unendlich groß. Es wäre demzufolge eine unendlich große Kraft erforderlich, um die für das Erreichen der Lichtgeschwindigkeit notwendige Beschleunigung aufzubringen. Eine solche unendlich große Kraft ist nicht realisierbar, die Lichtgeschwindigkeit demzufolge für einen Körper oder ein Teilchen nicht erreichbar.
Das Konzept führt aber auch zu Problemen:
- Der Erhaltungssatz der Masse aus der klassischen Physik gilt nicht mehr. Er gehört aber zum allgemeingültigen Energieerhaltungssatz. Rechnungen in der Teilchenphysik werden somit erschwert.
- Auch andere klassische Gesetze gelten nicht mehr. Beispielsweise verliert das zweite newtonsche Gesetz in der Form seine Richtigkeit. Eine allgemeine Formel für die Kraft muss über bestimmt werden.
- Mit der relativistischen bzw. der Ruhemasse wird eine zusätzliche physikalische Größe eingeführt. Das ist unübersichtlich und nicht notwendig.
Die Masse als relativ zu interpretieren führt also zu Vor- und Nachteilen. Im Alltag spielt der relativistische Anstieg von Trägheit und Schwere keine Rolle. In der Physik kann die relativistische Masse experimentelle Befunde anschaulich erklären, führt aber auch zu Problemen. In der Schule wird sie aufgrund ihrer Anschaulichkeit auch heute noch gern unterrichtet.
Ein Angebot von 